Relativistic Time Dilation in Muon Decay

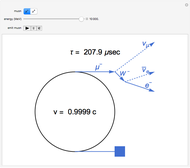
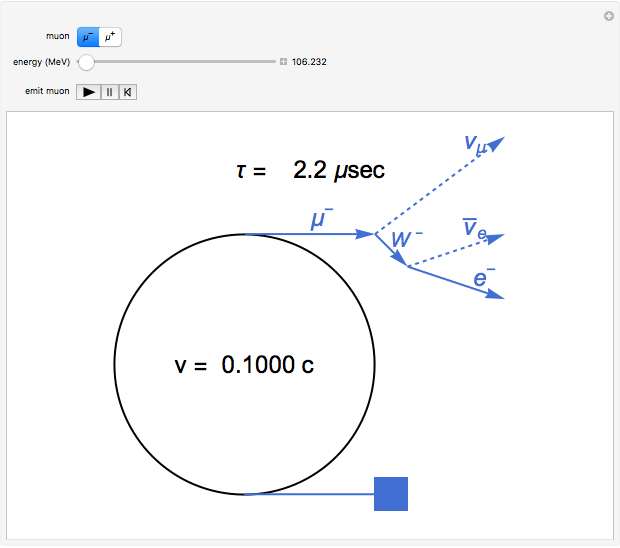
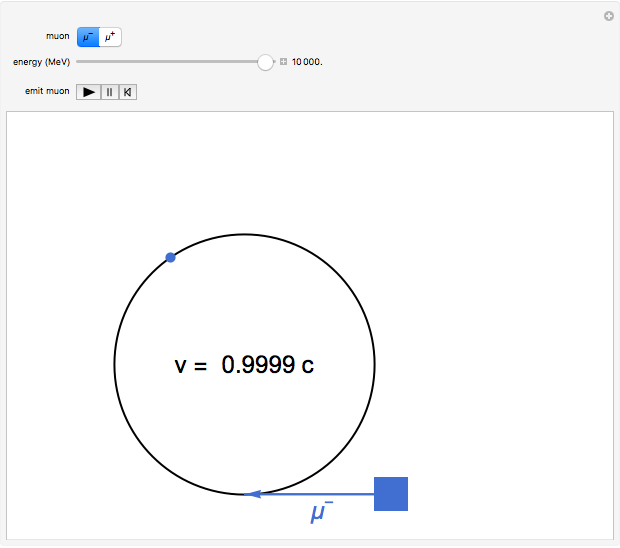
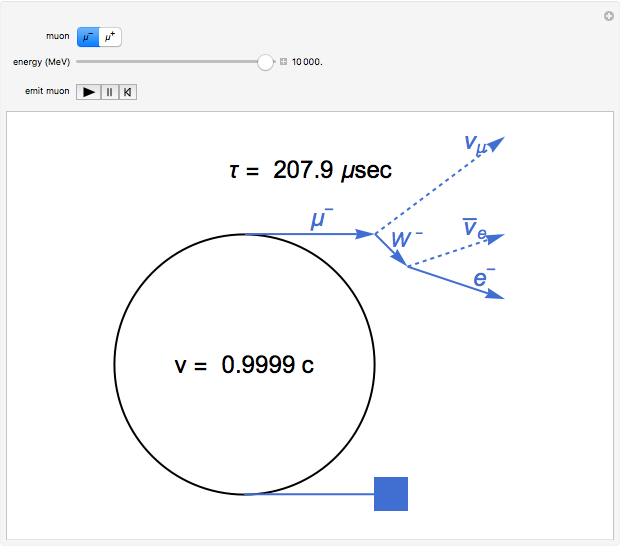
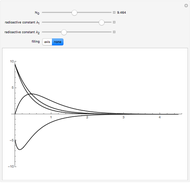
According to Einstein's special theory of relativity, a clock moving at a significant fraction of the speed of light with respect to an observer runs more slowly than the observer's own clock. This implies that time must be flowing more slowly in a moving frame of reference, which is referred to as time dilation. If a process (such as the decay of an unstable particle) occurs with an average lifetime of in the rest frame, the lifetime of the particle moving at speed is given by , where is the speed of light, 2.9979 × m/sec. The decay of muons has provided verification of Einstein's formula to a high degree of accuracy. The negative muon , with a mass of 105.7 MeV/, is the second-generation lepton analogous to the electron . The antiparticles and (the positron) are similarly related. The mean lifetime of free muon decay is 2.917 sec in the rest frame. The decay processes are and . Here is a neutrino and an antineutrino, each occurring in both electron and muon flavors. In finer detail, these weak-interaction processes involve bosons as intermediates.

High-energy collisions of protons produce copious numbers of pions, which, in turn, decay into muons. This all happens within the blue square in the graphic. The beam of muons thus produced is injected into a circular synchrotron, which can accelerate them to energies up to 10,000 MeV (10 GeV). The lifetimes are then determined as a function of energy. Muons accelerated to 750 MeV already travel at 99% the speed of light and have average lifetimes enhanced by an order of magnitude. At the maximum energy available in this Demonstration, speeds of 0.9999 are achieved and the muon lifetime is increased by a factor of 100.

Earlier experiments on muons produced by cosmic rays found their half-lives to be dependent on distance traveled through the atmosphere; they also exhibited relativistic time dilation.