General Equilibrium with Production: Robinson Crusoe with and without Trade

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
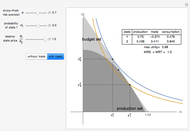
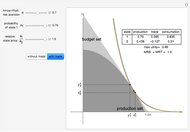
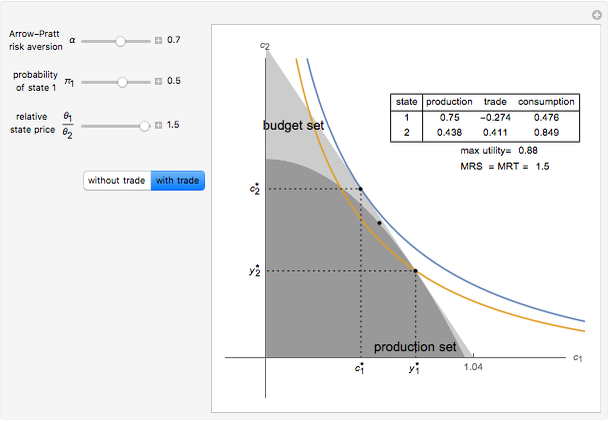
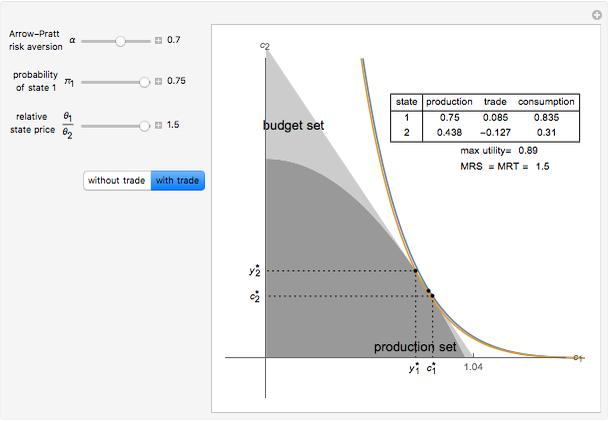
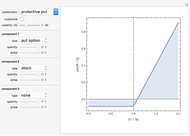
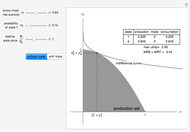
This Demonstration depicts the Robinson Crusoe production decision with two states of nature and one consumption good, with and without trade in Arrow–Debreu securities.
[more]
Contributed by: Tom Stannard and Graeme Guthrie (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 is Robinson's utility function, where
is Robinson's utility function, where  is the perceived probability of state
is the perceived probability of state  ,
,  is consumption in state
is consumption in state  , and
, and  is Robinson's level of Arrow–Pratt relative risk aversion. Robinson maximizes this function subject to the constraint that the production plan is feasible,
is Robinson's level of Arrow–Pratt relative risk aversion. Robinson maximizes this function subject to the constraint that the production plan is feasible,  .
.
If the production function is  (this function dictates the feasible production possibility set), and as stated previously,
(this function dictates the feasible production possibility set), and as stated previously,  (with no trade), then Robinson maximizes the function
(with no trade), then Robinson maximizes the function  with respect to
with respect to  to find the optimal state
to find the optimal state  consumption and production plan
consumption and production plan  . Given this,
. Given this,  . In equilibrium, the marginal rate of substitution (MRS) is equal to the marginal rate of transformation, which is equal to the slope of the indifference curve at the equilibrium point.
. In equilibrium, the marginal rate of substitution (MRS) is equal to the marginal rate of transformation, which is equal to the slope of the indifference curve at the equilibrium point.
When trade is introduced, the maximization methodology is consistent with that of the no-trade case. However, now Robinson chooses  and
and  to maximize
to maximize  , subject to the constraints that production is feasible,
, subject to the constraints that production is feasible,  , and consumption is affordable,
, and consumption is affordable,  . This results in a boundary of possible consumption plans (the budget line) that is a straight line running through the production plan with a slope
. This results in a boundary of possible consumption plans (the budget line) that is a straight line running through the production plan with a slope  (the relative state price).
(the relative state price).
References
[1] H. Varian, Intermediate Microeconomics: A Modern Approach, 8th ed., New York: W. W. Norton, 2009.
[2] R. Starr, General Equilibrium Theory: An Introduction, 2nd ed., New York: Cambridge University Press, 2011.
Permanent Citation