Generating All Coprime Pairs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
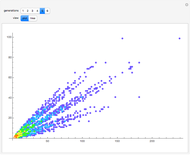
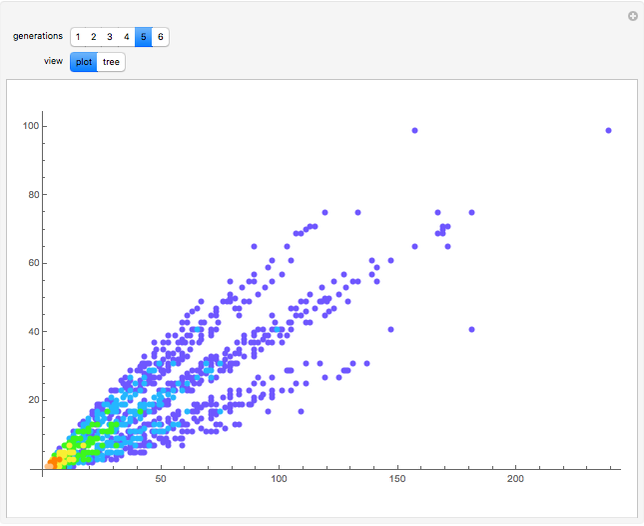
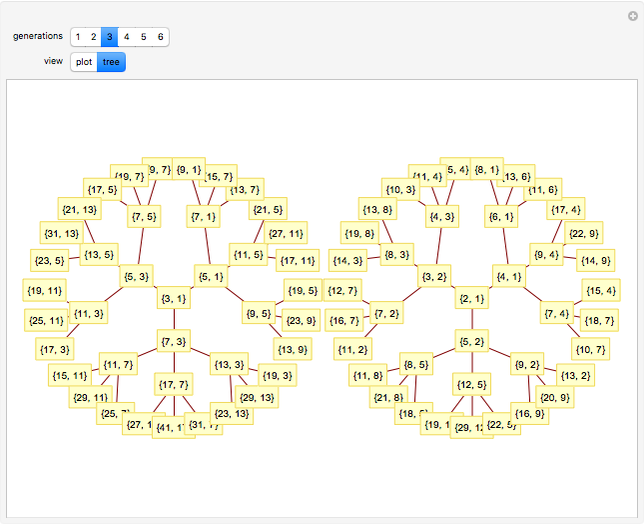
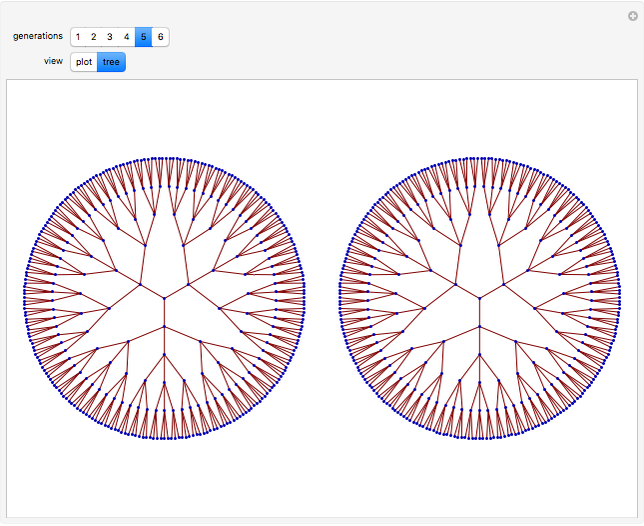
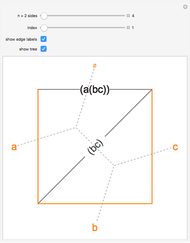
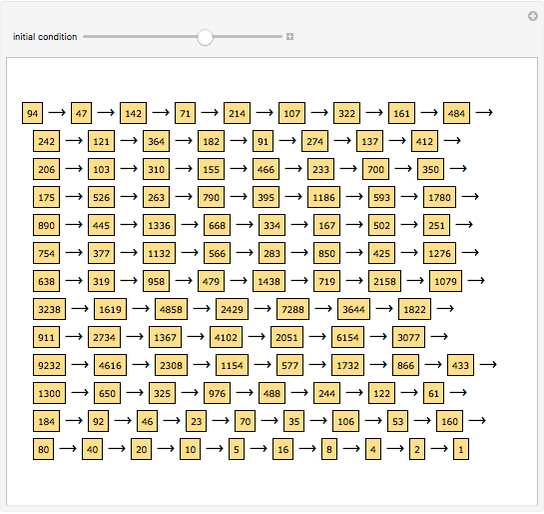
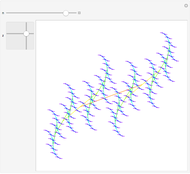
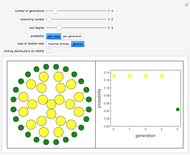
Two integers are said to be coprime (or relatively prime) if they do not share a common divisor different than 1. For instance, 4 and 9 are coprime (no common divisor except 1), but 12 and 15 are not (common divisor 3). The plot shows generations of coprime pairs 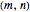 , starting from
, starting from  and
and  , where three new pairs are produced at each step:
, where three new pairs are produced at each step:  ,
,  , and
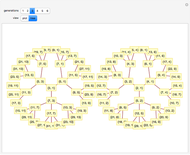
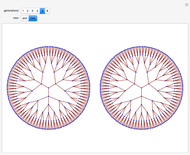
, and  . The resulting triplets can be arranged in two complete ternary trees. The procedure described here generates all coprime pairs without repetition; the colors represent the different generations.
. The resulting triplets can be arranged in two complete ternary trees. The procedure described here generates all coprime pairs without repetition; the colors represent the different generations.
Contributed by: Enrique Zeleny (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Wikipedia. "Coprime Integers." (Sep 26, 2012) en.wikipedia.org/wiki/Coprime_integers.
Permanent Citation
"Generating All Coprime Pairs"
http://demonstrations.wolfram.com/GeneratingAllCoprimePairs/
Wolfram Demonstrations Project
Published: September 27 2012