Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

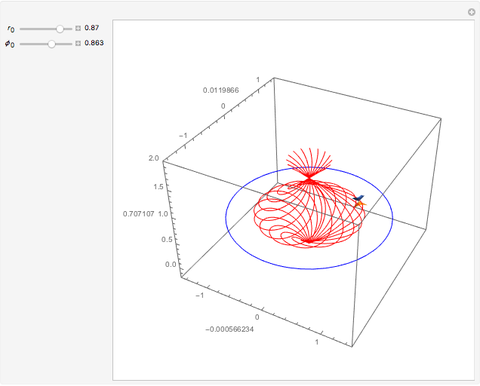
Gödel's Universe

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

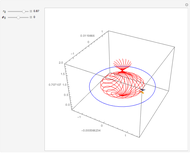
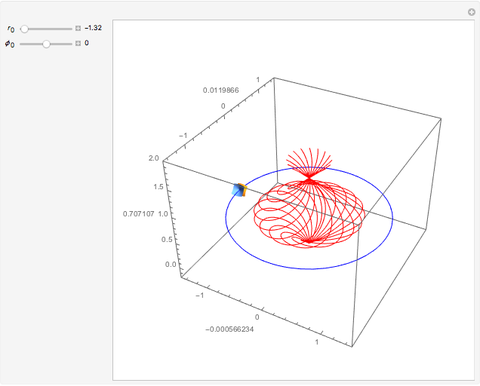
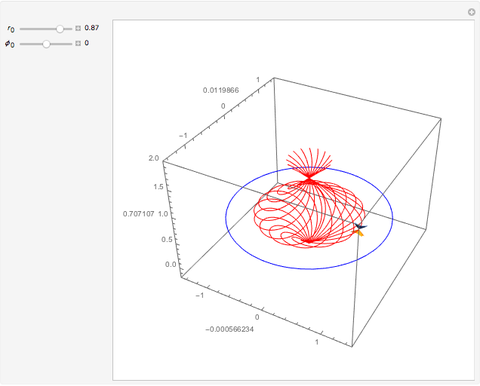
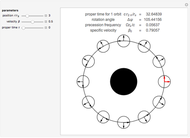
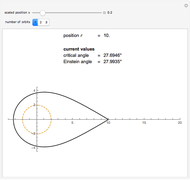
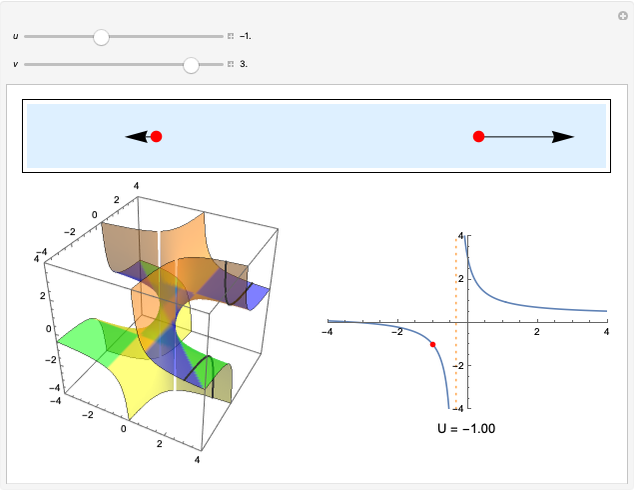
In 1949, Kurt Gödel found a solution of Einstein's field equations and gave it to Einstein on his birthday [1]. This solution describes a homogeneous, anisotropic, and rotationally symmetric spacetime in which matter takes the form of a pressure-free perfect fluid with negative cosmological constant, where closed timelike world lines exist. Theoretically, traveling along such a world line allows an observer to travel into their own past. For an astounding and detailed visualization of how an observer would perceive such a travel, see [2, 3].

[more]

The manipulate graphic reproduces the famous illustration contained in the book by Hawking and Ellis [4], showing photons emitted by an observer on the axis of symmetry at the bottom; the photons spiral out, expand, and reconverge at the top. Light-like geodesics are shown as well as light cones that tip as you increase producing the closed timelike curves. Further interpretations can be found in [5].

[less]

Contributed by: Enrique Zeleny (August 2013)
Based on a program by: Torsten Schönfeld
Open content licensed under CC BY-NC-SA

Snapshots

Details

In cylindrical-polar coordinates , Gödel's metric is given by

,

where is a constant. The coordinate does not appear in the metric.

References

[1] W. Rindler, “Gödel, Einstein, Mach, Gamow, and Lanczos: Gödel’s Remarkable Excursion into Cosmology,” American Journal of Physics, 77(6), 2009 pp. 498–510. doi:10.1119/1.3086933.

[2] M. Buser, E. Kajari, and W. P. Schleich, "Visualization of the Gödel Universe," New Journal of Physics, 15, 2013 013063. doi:10.1088/1367-2630/15/1/013063.

[3] S. Ceurstemont, "First Time-Travel Movies Reveal Surreal Universe," New Scientist TV (blog). (Jan 2013) www.newscientist.com/blogs/nstv/2013/01/first-time-travel-movies-reveal-surreal-universe.html.

[4] S. Hawking and G. F. R. Ellis, The Large Scale Structure of Space-Time, Cambridge: Cambridge University Press, 1973 section 5.7.

[5] I. Németi, J. X. Madarász, H. Andréka, and A. Andai, "Visualizing Ideas about Gödel-Type Rotating Universes," in Gödel-Type Spacetimes: History and New Developments (M. Scherfner and M. Plaue, eds.). Kurt Gödel Society: Collegium Logicum X, 2010 pp. 77–127. www.math-inst.hu/pub/algebraic-logic/godunivisu-revised.pdf.

[6] T. Schönfeld. "GeodesicGeometry." (Aug 10, 2013) www.math-inst.hu/pub/algebraic-logic/godunivisu-revised.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send