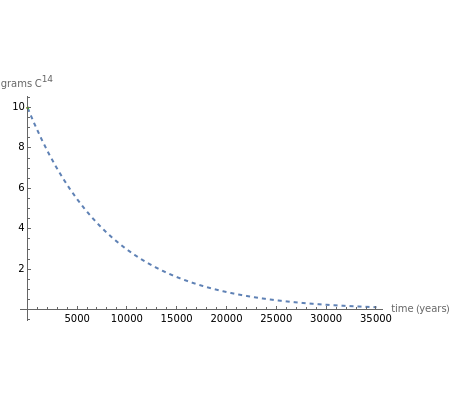
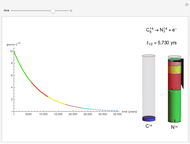
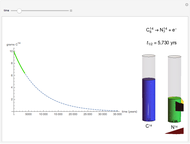
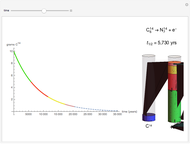
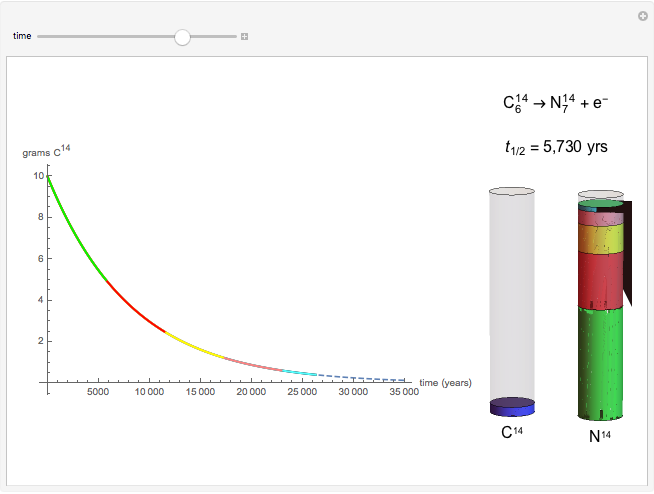
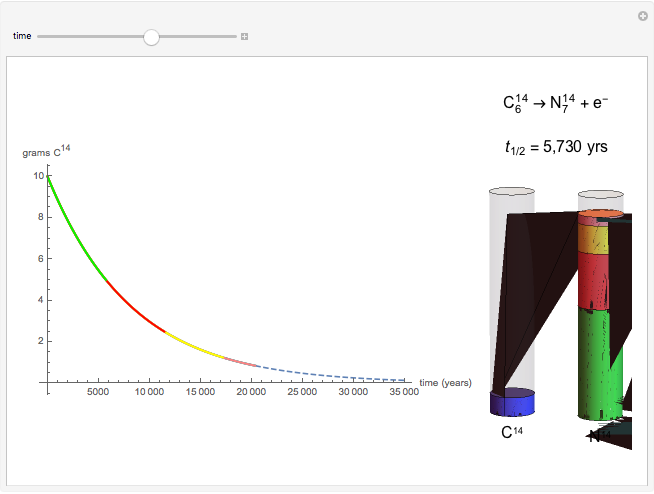
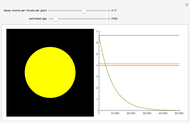
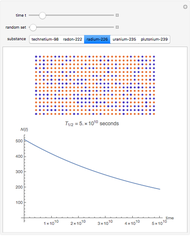
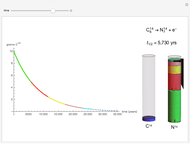
The half-life of a reaction is the time required for the amount of reactant to decrease by a half. The half-life of a first-order reaction is a constant, so each successive half-life represents an equal period of time. For example, carbon-14 decays to nitrogen-14 by the emission of an electron with a half-life of 5,730 years. This Demonstration illustrates how an initial sample of 10 grams of carbon-14 decays to nitrogen-14 over 34,380 years.