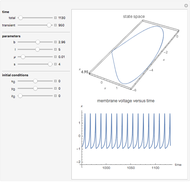
Hindmarsh-Rose Neuron Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
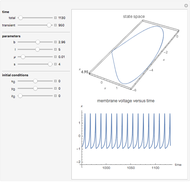
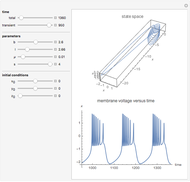
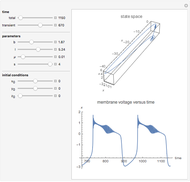
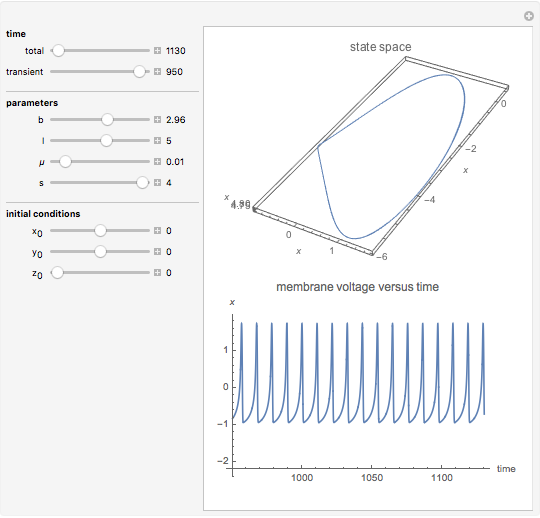
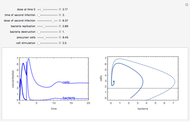
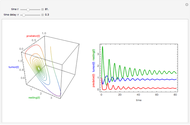
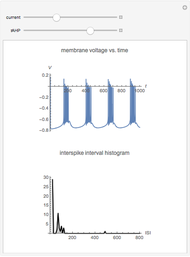
The phenomenological neuron model proposed by Hindmarsh and Rose may be seen either as a generalization of the Fitzhugh equations or as a simplification of the physiologically realistic model proposed by Hodgkin and Huxley. It is capable of mimicking almost all the behaviors exhibited by real biological neurons, such as spiking, bursting, and irregular behaviors.
[more]
Contributed by: Daniele Linaro, Marco Storace, and Enno de Lange (March 2011)
Open content licensed under CC BY-NC-SA
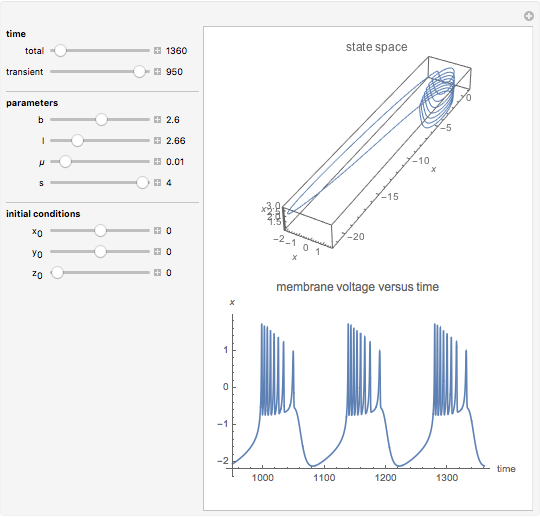
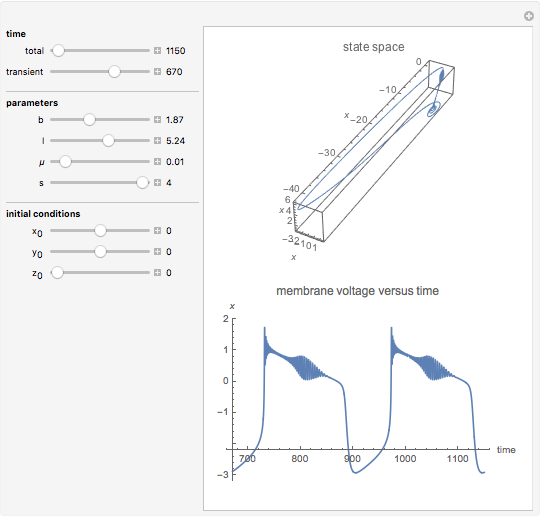
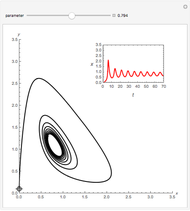
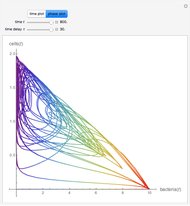
Snapshots
Details
The roles played by the system parameters are the following:  mimics the membrane input current for biological neurons;
mimics the membrane input current for biological neurons;  allows one to switch between bursting and spiking behaviors and to control the spiking frequency;
allows one to switch between bursting and spiking behaviors and to control the spiking frequency;  controls the speed of variation of the slow variable;
controls the speed of variation of the slow variable;  governs adaptation: a unitary value of
governs adaptation: a unitary value of  determines spiking behavior without accommodation and subthreshold adaptation, whereas values around 4 give strong accommodation and subthreshold overshoot.
determines spiking behavior without accommodation and subthreshold adaptation, whereas values around 4 give strong accommodation and subthreshold overshoot.
Two-dimensional bifurcation diagrams can be found in the following paper:
M. Storace, D. Linaro, and E. de Lange, "The Hindmarsh-Rose Neuron Model: Bifurcation Analysis and Piecewise-Linear Approximations," Chaos, 18, 2008 pp. 1–10 033128.
More information on the model and on its bifurcations can be found on our research page.
Permanent Citation
"Hindmarsh-Rose Neuron Model"
http://demonstrations.wolfram.com/HindmarshRoseNeuronModel/
Wolfram Demonstrations Project
Published: March 7 2011