Chaos in Tumor Growth Model with Time-Delayed Immune Response

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
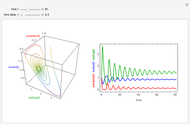
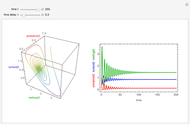
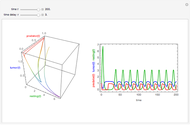
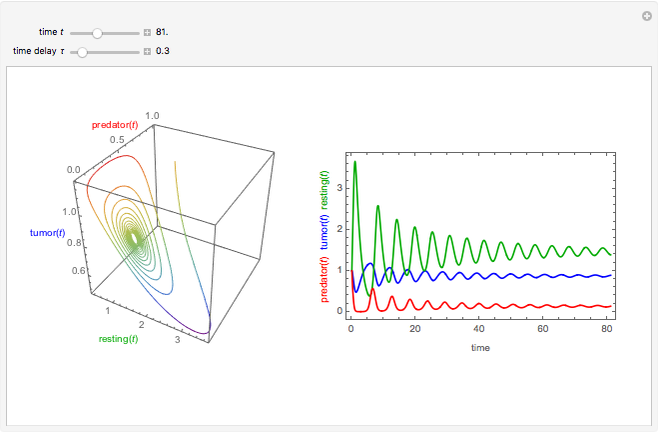
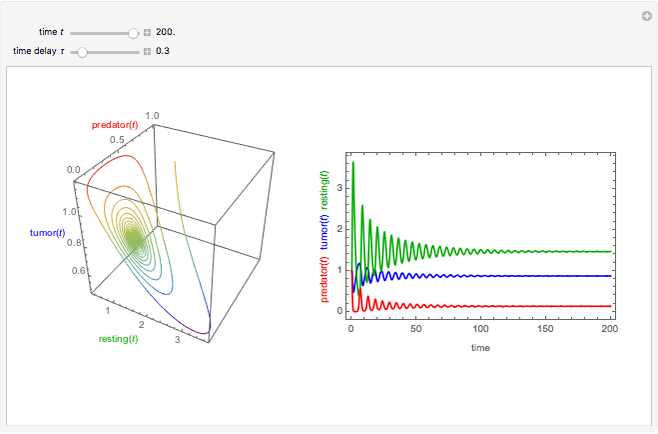
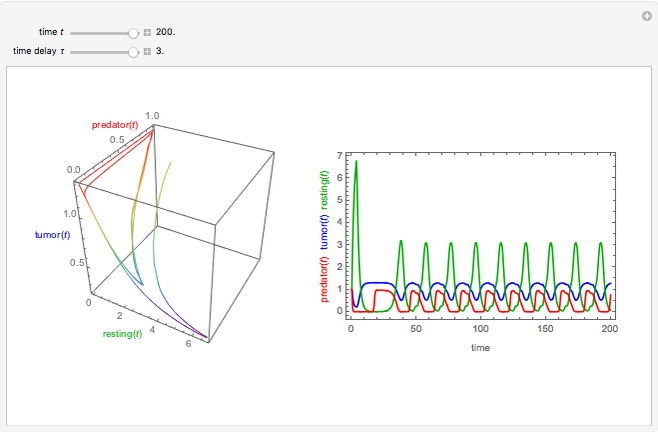
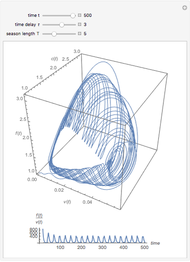
This Demonstration considers a tumor growth model in which tumor cells play the role of prey, and the immune system is represented by resting and predator cells.
[more]
Contributed by: Clay Gruesbeck (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] M. Saleem and T. Agrawal, "Chaos in a Tumor Growth Model with Delayed Responses of the Immune System," Journal of Applied Mathematics, #891095, 2012 pp. 1–16. doi:10.1155/2012/891095.
[2] R. H. Thomlinson "Measurement and Management of Carcinoma of the Breast," Clinical Radiology, 33(5), 1982 pp. 481–493.
Permanent Citation