Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

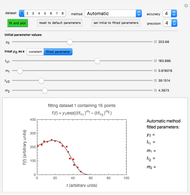
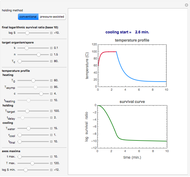
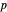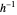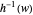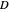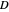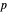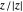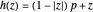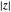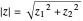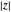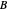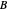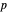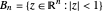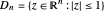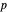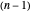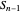Homeomorphism of a Disk Mapping the Origin to Another Interior Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

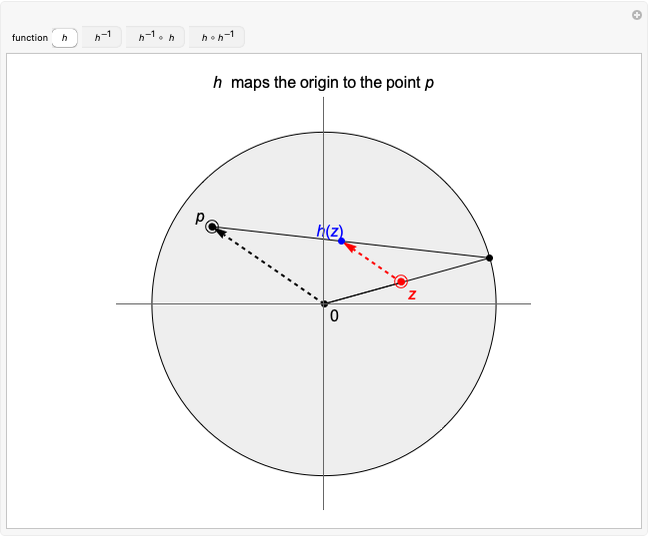
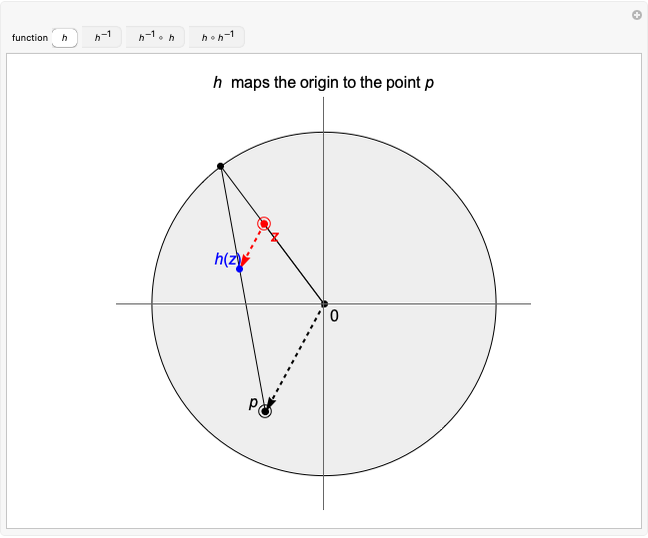
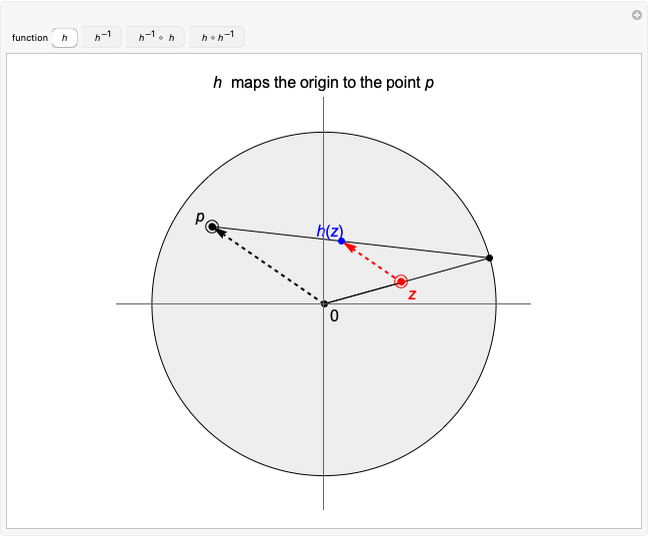
This Demonstration shows the action of a homeomorphism 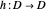of the closed unit disk in the plane that maps the origin 0 to a selected point in the open unit disk 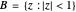, while keeping each point on the boundary of 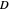fixed. It also shows the action of the inverse 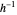of as well as of the compositions 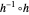and .

[more]

Drag the point to the desired location; that determines the homeomorphism . Drag the point around inside the disk to see the corresponding point given by the homeomorphism.

Similarly, select the button to see the locator for the point . Drag around inside the disk to see the corresponding point given by the inverse of the homeomorphism .

To say that is an homeomorphism of means that it is a one-to-one continuous function that maps onto and whose inverse function is also continuous.

For a point , the function maps the radial line segment from 0 to linearly onto the line segment from to . Such an is given by the formula , where denotes the Euclidean norm of , that is, or, what is the same thing, is the modulus of the complex number .

A consequence of what is shown here is that the open unit disk is homogeneous in the sense that given any two points in , there is a homeomorphism of mapping one of the points to the other. An alternative way to obtain the same result is to use a Möbius transformation, that is, a linear fractional transformation, as indicated in [1].

The method used here generalizes to any number of dimensions: given a point in the open unit -ball in -dimensional Euclidean space , there is a homeomorphism of the corresponding closed unit -disk that maps the origin to while keeping each point of the bounding -sphere fixed. Consequently, the open unit -ball is homogeneous.

[less]

Contributed by: Murray Eisenberg (June 13)
With additional contributions by: Mark D. Normand
Open content licensed under CC BY-NC-SA

Details

Snapshot 1: image under the homeomorphism of another point in the open disk for the same point 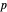seen in the Thumbnail image

Snapshot 2: image under of a point in the open disk but for a different given point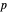

Snapshot 3: image under of the origin is the given point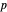

Snapshot 4: image under of a point on the bounding circle is the same as

Snapshot 5: image under the inverse homeomorphism of a point in the open disk for a given point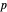

Snapshot 6: image under 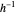of another point 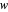in the open disk for the same point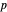

Snapshot 7: image under 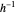of a point in the open disk but for a different point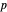

Snapshot 8: image under 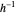of the given point is the origin

Snapshot 9: image under 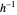of a point 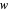on the bounding circle is the same as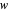

References

[1] Mathematics Stack Exchange. "Conformal Automorphism of Unit Disk That Interchanges Two Given Points." (Mar 4, 2022). math.stackexchange.com/a/3093167.

[2] J. M. Lee, Introduction to Topological Manifolds, 2nd ed., New York: Springer, 2011.

[3] Mathematics Stack Exchange. "A Homeomorphism of Fixing the Boundary?" (Mar 4, 2022). math.stackexchange.com/a/1517119.

[4] Mathematics Stack Exchange. " 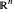 Is a Strongly Locally Homogeneous Space." (Mar 4, 2022). math.stackexchange.com/a/4066088.

[5] M. Eisenberg, Topology, New York: Holt, Rinehart and Winston, 1974.

[6] E. W. Weisstein. "Homeomorphism" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/Homeomorphism.html (Wolfram MathWorld).

[7] E. W. Weisstein. "Disk" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/Disk.html (Wolfram MathWorld).

[8] E. W. Weisstein. "Linear Fractional Transformation" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/LinearFractionalTransformation.html (Wolfram MathWorld).

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send