Brouwer Fixed Point Theorem

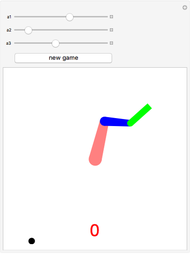
Drag the endpoints of the line. As long as no part of the dragged line falls outside of the range of the original line, at least one point will always lie at its original horizontal position, as shown by the indicator. The gray value of that point will match the gray of the background exactly. Try as hard as you like to find a dragged position where no point is in its original horizontal position; you will not succeed. The Brouwer fixed point theorem guarantees that.