Interference of Waves from Double Slit (Young's Experiment)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
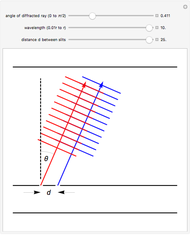
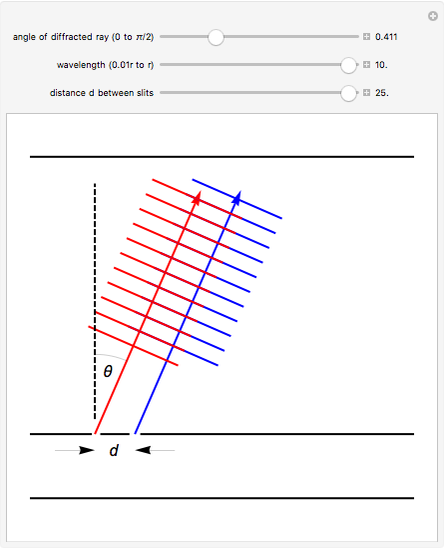
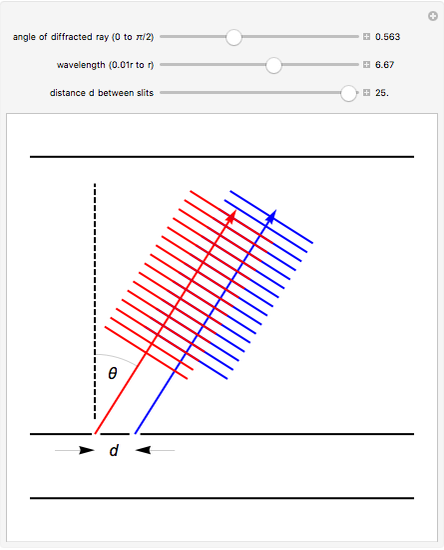
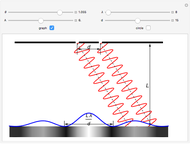
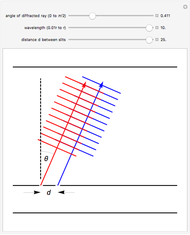
Thomas Young observed interference of light and measured the wavelength of light in this classic experiment, performed around 1801. It provided the clinching evidence in Young's arguments for the wave model for light. This Demonstration shows two light waves of the same wavelength (shown in red and blue for ease of viewing) which have passed through two narrow slits and, as a result of diffraction, are traveling at an angle  to their original direction of propagation. At the angle shown above, red and blue wave crests alternate and cancel, resulting in a dark spot on the screen. At other angles
to their original direction of propagation. At the angle shown above, red and blue wave crests alternate and cancel, resulting in a dark spot on the screen. At other angles 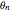 , red and blue crests fall on top of one another and reinforce, resulting in a bright spot on the screen. The user can vary the angle
, red and blue crests fall on top of one another and reinforce, resulting in a bright spot on the screen. The user can vary the angle  , the wavelength
, the wavelength 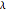 , and the distance between the slits
, and the distance between the slits  to see how changes in the three variables affect the interference pattern formed by the two waves. The "double slit" formula
to see how changes in the three variables affect the interference pattern formed by the two waves. The "double slit" formula 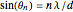 relates
relates 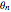 ,
, 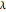 ,
, 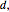 and
and  , the number of wavelengths difference in the path length of the two waves.
, the number of wavelengths difference in the path length of the two waves.
Contributed by: Fernand Brunschwig (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
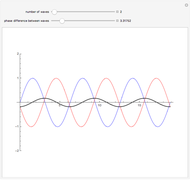
Snapshot 1: The red and blue wave crests fall on top of each other and thus reinforce each other, which would result in a bright spot on the screen at this angle. The blue waves are one full wavelength "ahead of" the red waves.
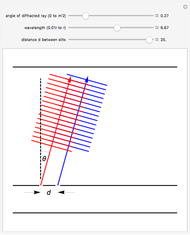
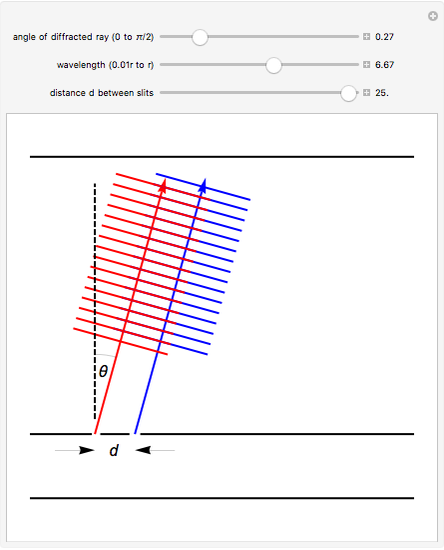
Snapshot 2: The wavelength is smaller than in Snapshot 1. As a result, the angle at which the red and blue wave crests fall on top of each other must also be smaller. As in Snapshot 1, this would result in a bright spot on the screen at this angle. The blue waves are one full wavelength "ahead of" the red waves.
Snapshot 3: The wavelength and slit width are the same as in Snapshot 2. However, the angle is much larger and the wave crests are still falling on top of each other. This is the result of the fact that the blue waves are now two full wavelengths "ahead of" the blue waves.
Inspired by "The Wave Theory," Chap. 6 in R. Karplus, Introductory Physics: A Model Approach, 2nd ed., Buzzards Bay, MA: Captain's Engineering Services, Inc., 2003.
Permanent Citation
"Interference of Waves from Double Slit (Young's Experiment)"
http://demonstrations.wolfram.com/InterferenceOfWavesFromDoubleSlitYoungsExperiment/
Wolfram Demonstrations Project
Published: March 7 2011