Is There a Klein Paradox in Graphene?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
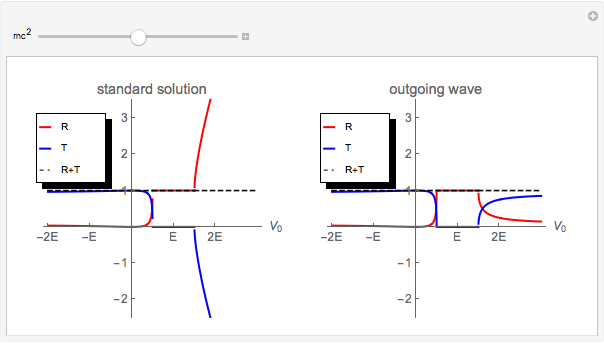
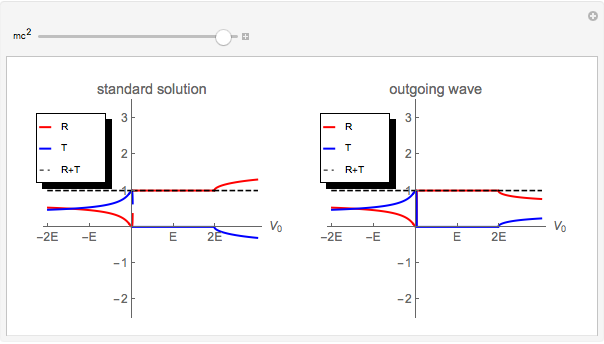
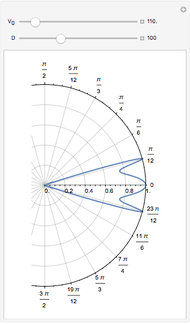
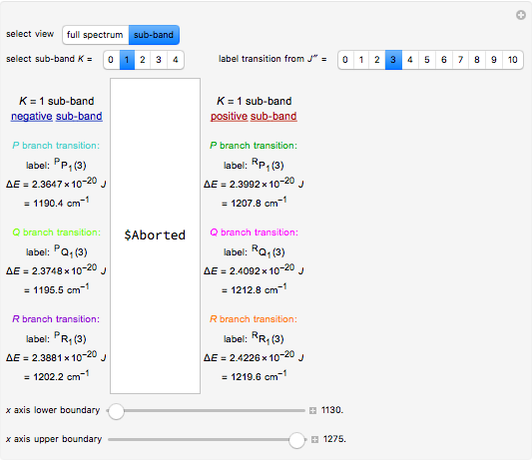
This Demonstration shows the reflection and transmission coefficients for a Dirac particle with spin up and mass 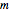 impinging on a sharp semi-infinite barrier of variable height
impinging on a sharp semi-infinite barrier of variable height 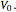 On the left we have the standard solution; on the right we have imposed the alternative boundary condition that for all energies the transmitted wave moves to the right. All energies
On the left we have the standard solution; on the right we have imposed the alternative boundary condition that for all energies the transmitted wave moves to the right. All energies 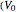 and
and 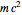 ) are expressed in terms of the fixed incoming energy
) are expressed in terms of the fixed incoming energy 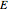 . You are invited to vary the mass
. You are invited to vary the mass 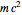 , and especially look at the limit of zero mass (of relevance in graphene).
, and especially look at the limit of zero mass (of relevance in graphene).
Contributed by: Niels Walet (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
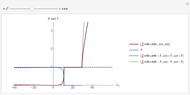
There is more than one way to interpret the scattering by a Dirac electron from a half-infinite barrier, that is, in which one-half of space, assumed to be on the right-hand side, is at a raised potential 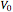 . The traditional way, as first set out by Klein in [1], is to use the same solution for positive energy states on the left and positive or negative energy states on the right. This leads to the famous Klein paradox (see, e.g., Sakurai [2]): when
. The traditional way, as first set out by Klein in [1], is to use the same solution for positive energy states on the left and positive or negative energy states on the right. This leads to the famous Klein paradox (see, e.g., Sakurai [2]): when 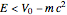 there is a negative flow of transmitted particles and a probability of reflection greater than one. This is interpreted as the creation of particle-antiparticle pairs, where the negative transmission coefficient just shows the flux of antiparticles to the right. The "standard solution" shows exactly this behavior.
there is a negative flow of transmitted particles and a probability of reflection greater than one. This is interpreted as the creation of particle-antiparticle pairs, where the negative transmission coefficient just shows the flux of antiparticles to the right. The "standard solution" shows exactly this behavior.
In recent years, the Dirac equation has been realized in graphene, and the scattering of a finite barrier in such a system has been discussed in [3]. As long as we look at a finite-width barrier there is no room for argument, but if we look at a half-infinite barrier (or "n-p" graphene) we need to apply a different boundary condition; since the Fermi surface of both types of graphene lies at the same energy below that of the conducting electron, we need to impose outgoing particle boundary conditions on the right hand side. As can be shown (see, e.g., [4]) this leads to a trivial modification of the expression for 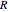 and
and  , with the consequence that
, with the consequence that  ,
, 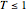 for all energies. This is shown in the panel on the right. We conclude that, depending on the boundary condition, there is either a Klein paradox that can be resolved by invoking a reservoir of occupied negative energy states that can be accessed, or no Klein paradox if we assume that we have no such reservoir, since the boundary conditions on the side of the barrier depend on this choice. Thus we may argue whether the Klein paradox is real.
for all energies. This is shown in the panel on the right. We conclude that, depending on the boundary condition, there is either a Klein paradox that can be resolved by invoking a reservoir of occupied negative energy states that can be accessed, or no Klein paradox if we assume that we have no such reservoir, since the boundary conditions on the side of the barrier depend on this choice. Thus we may argue whether the Klein paradox is real.
References:
[1] O. Klein, "Die Reflexion von Elektronen an Einem Potentialsprung Nach der Relativistischen Dynamik von Dirac," Z. Phys., 53(3–4), 1929 pp. 157–165.
[2] J. J. Sakurai, Advanced Quantum Mechanics, New York: Addison-Wesley, 1967.
[3] M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, "Chiral Tunnelling and the Klein Paradox in Graphene," Nature Physics, 2, 2006 pp. 620–625.
[4] D. Dragoman, "Evidence Against the Klein Paradox in Graphene," Phys. Scr., 79(1), 2009.
Also see the Wikipedia entry for Klein paradox.
Permanent Citation