Iso-n Triangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
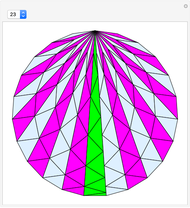
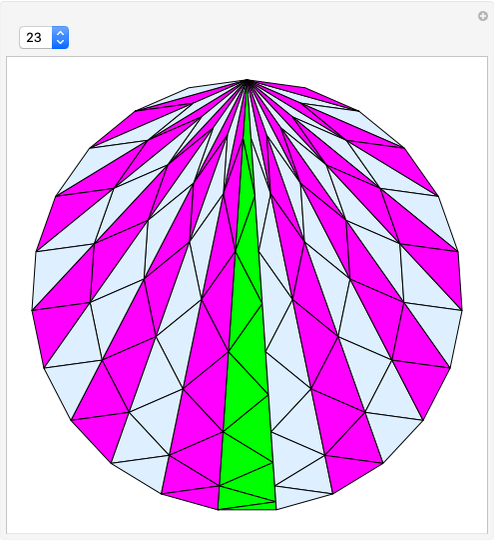
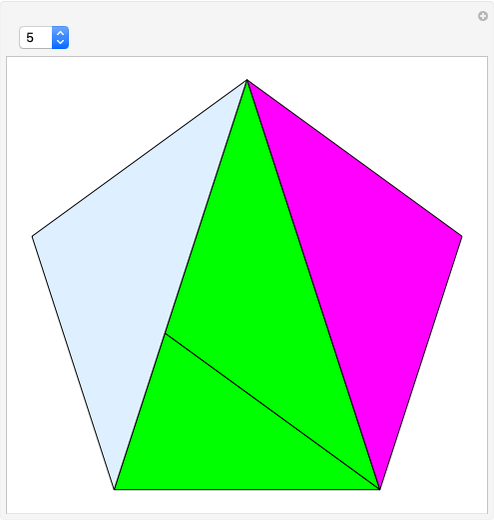
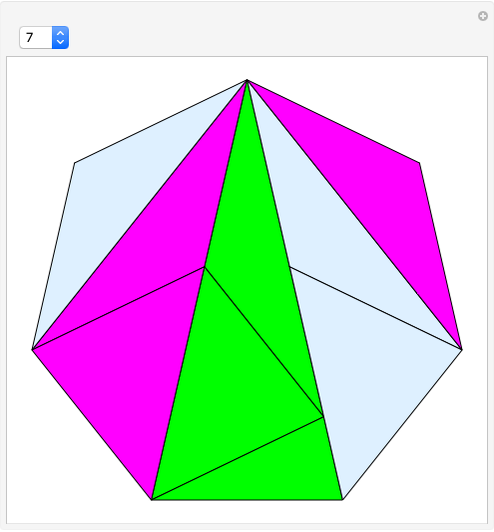
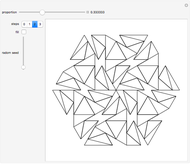
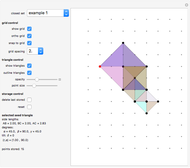
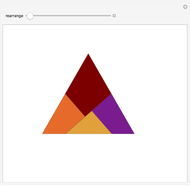
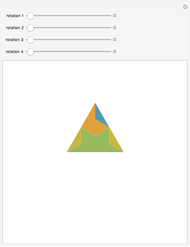
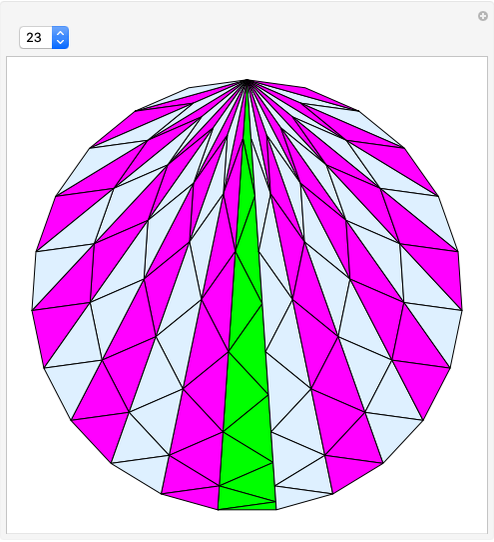
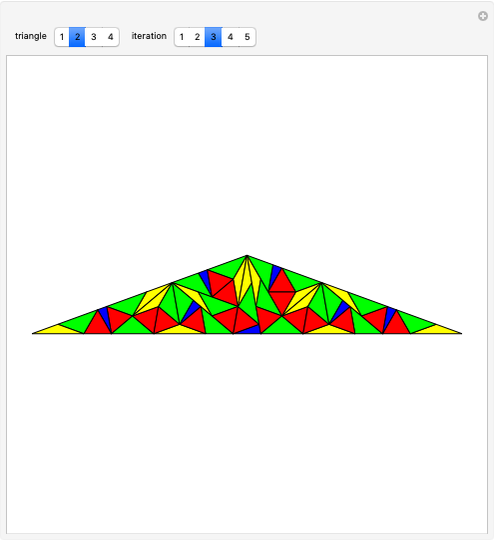
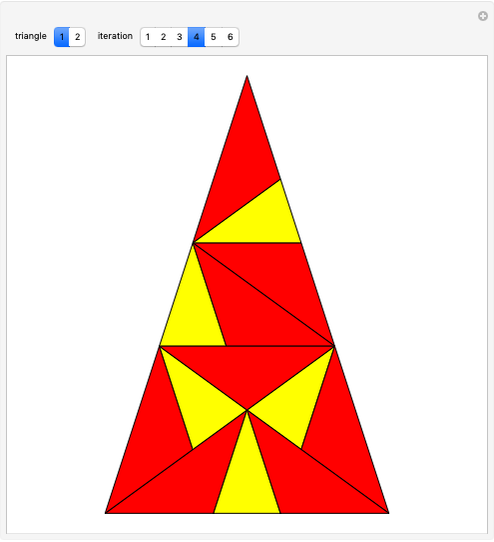
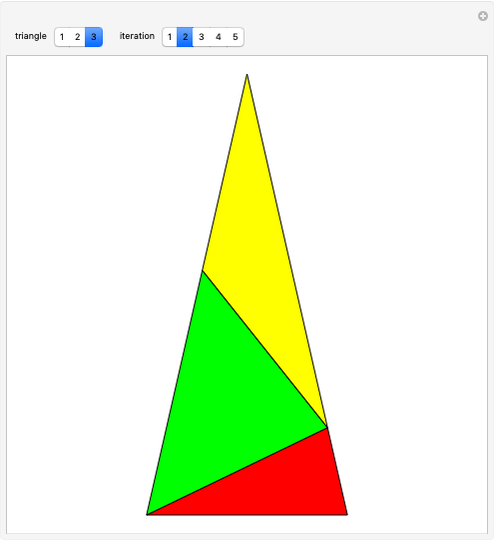
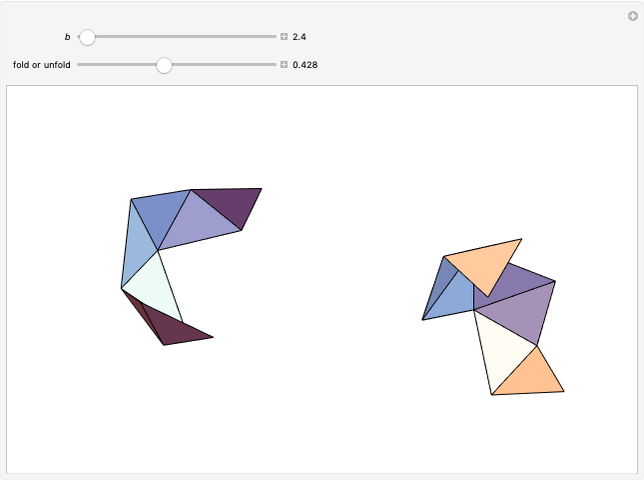
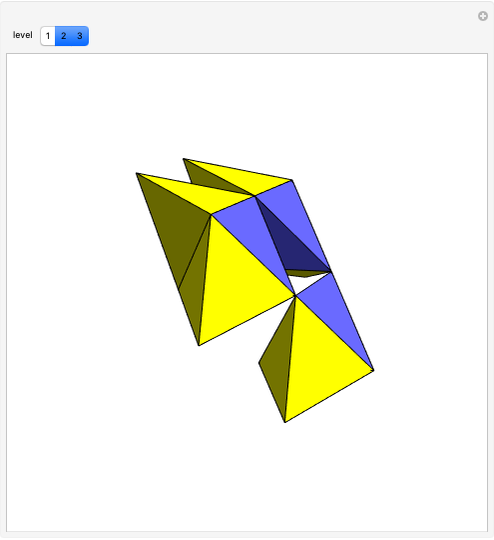
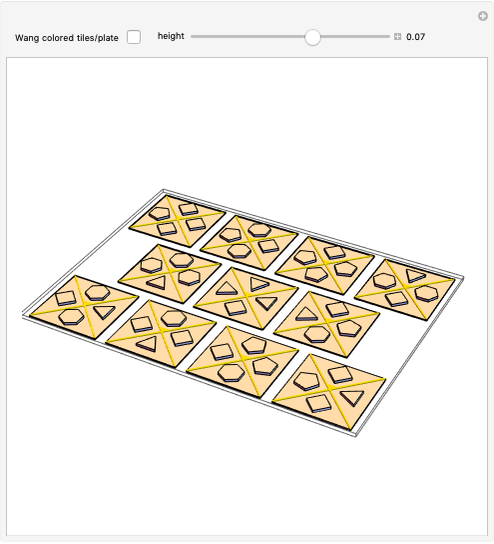
This Demonstration shows the dissection of a regular  -gon into iso-
-gon into iso- triangles (
triangles ( is an odd integer greater than 1).
is an odd integer greater than 1).
Contributed by: Izidor Hafner (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
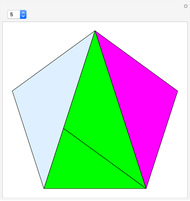
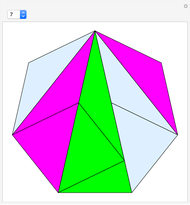
If a regular polygon has an odd number of sides, then it can be dissected into isosceles triangles with the same legs. These triangles have certain kinds of angles. Specifically, a regular polygon with  sides contains
sides contains  isosceles triangles whose third angle equals
isosceles triangles whose third angle equals  , for
, for  [1, p. 11]. For the pentagon, Frederickson calls these triangles iso-penta triangles [1, p. 212] and for the heptagon, they are called iso-hepta triangles [1, p. 218]. So in the case of the regular
[1, p. 11]. For the pentagon, Frederickson calls these triangles iso-penta triangles [1, p. 212] and for the heptagon, they are called iso-hepta triangles [1, p. 218]. So in the case of the regular  -gon, we call them iso-
-gon, we call them iso- triangles.
triangles.
Reference
[1] G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 1997.
Permanent Citation