Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Sturm's Theorem for Polynomials

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

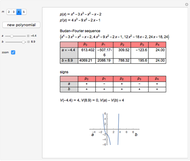
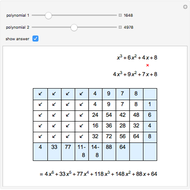
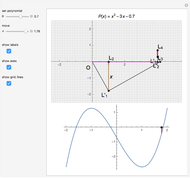
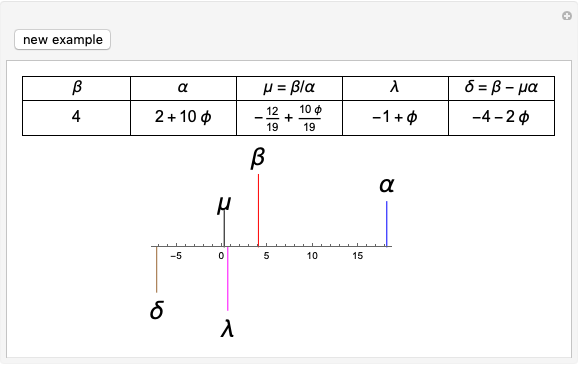
Let be the number of real roots of an algebraic equation with real coefficients whose real roots are simple over an interval and are not or . Then , the difference between the number of sign changes of the Sturm chain evaluated at and at .

[more]

By subdividing an interval until every subinterval contains at most one root, one can locate subintervals containing all the real roots in the original interval.

[less]

Contributed by: Izidor Hafner (January 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

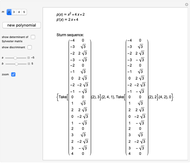
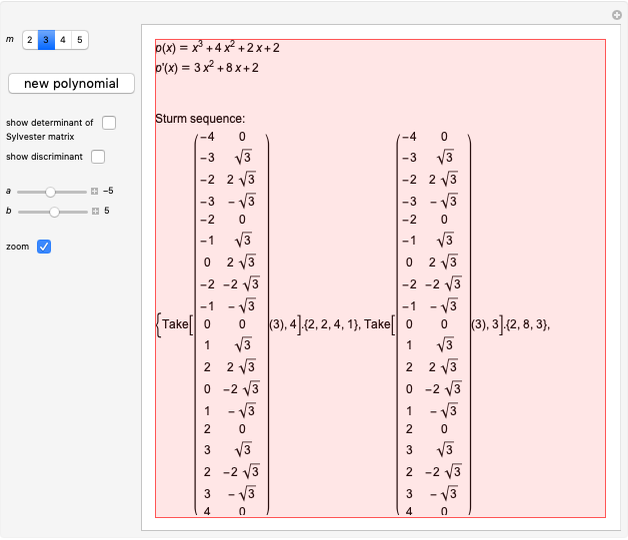
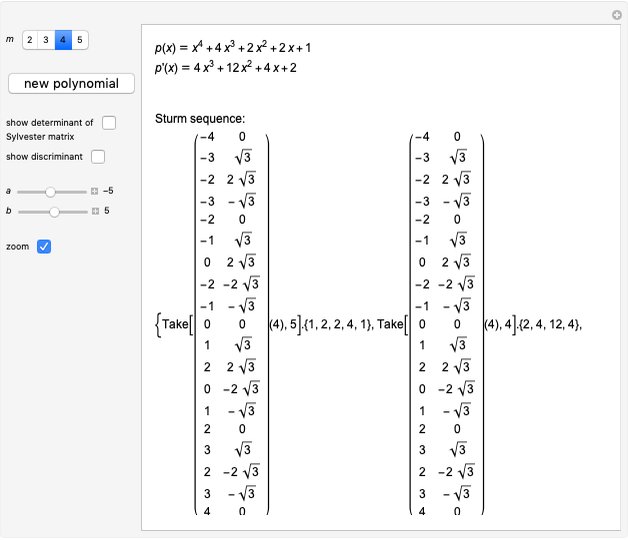
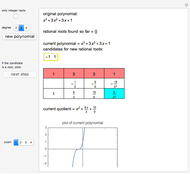
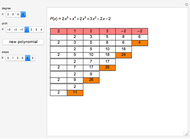
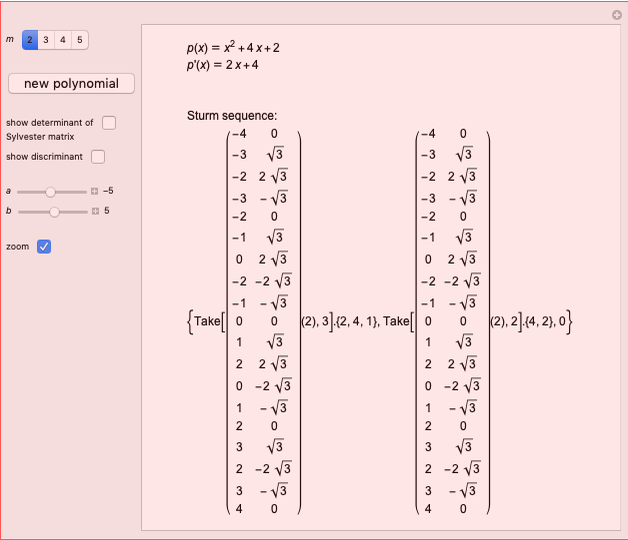
The Sturm chain of a polynomial is the sequence of polynomials:

,

where

p2(x)= q1(x)p1(x)-p0(x),&IndentingNewLine;p3(x)=q2(x)p2(x)-p1(x),&IndentingNewLine;…&IndentingNewLine;ps(x)=qs-1(x)ps-1(x)-ps-2(x).

Here and are the polynomial quotient and remainder of . The chain ends when the polynomial is a constant.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send