Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Joule Wire Heater

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

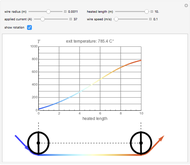
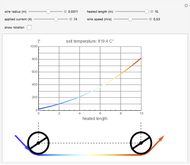
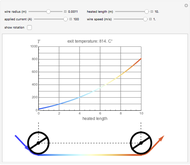
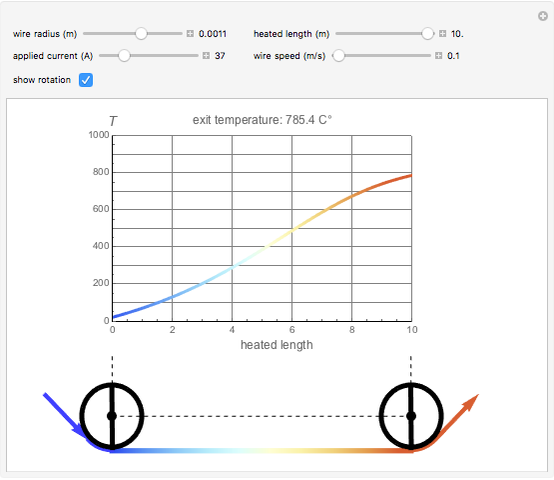
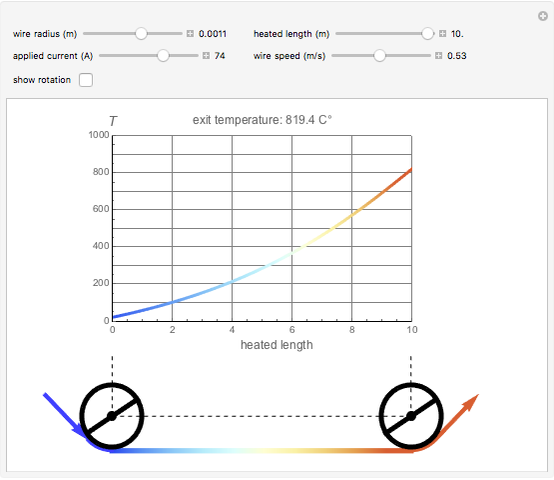
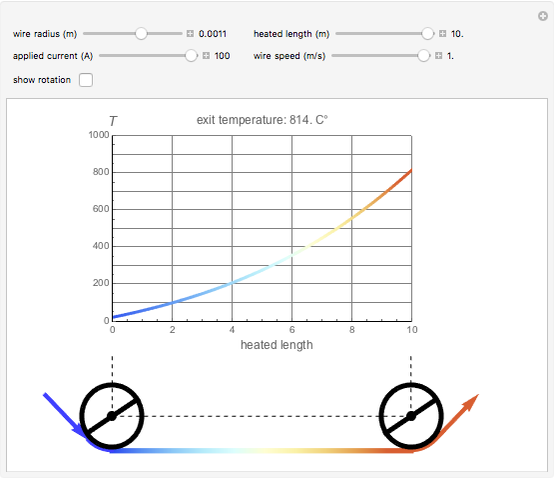
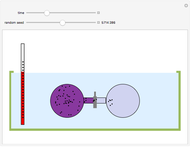
Steel wire can be heated by passing an electric current through it. In practice, this can be achieved by running the wire over two rollers to which an electric potential is applied. This is an application of Joule's first law: the heat (energy) produced is proportional to the square of the current multiplied by the electrical resistance of the wire, . This heat, minus the energy loss due to radiation, produces a temperature rise in the wire.

[more]

This Demonstration shows the temperature rise as a function of the system parameters: wire radius, wire speed, heated length, and applied current.

[less]

Contributed by: Erik Mahieu (November 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

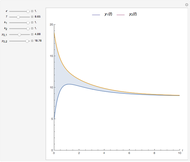
The temperature at the second roller (the exit) can be calculated by solving the differential equation representing the energy equilibrium of the system:
 ,

where

is the temperature coefficient of resistivity of steel: .005 , is the specific heat of steel: 0.45 , is the Stefan–Boltzmann constant: 5.670373 , is the density of steel: 7.9 , is the specific resistivity of steel: 1.7 ,

The three snapshots illustrate how the same temperature can be reached with different combinations of current speed. Which one to use is determined by economic considerations.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send