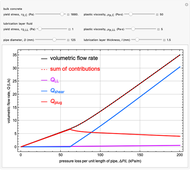
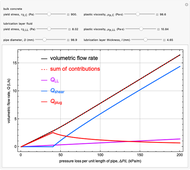
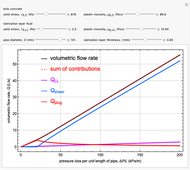
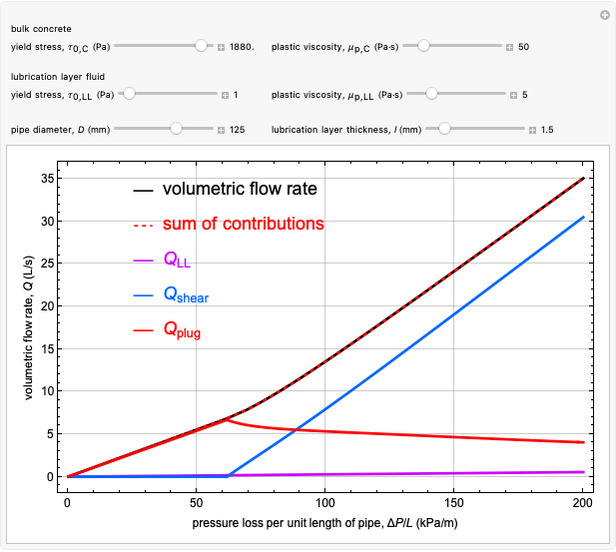
Khatib-Khayat Model for Pumping Flowable Concrete

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
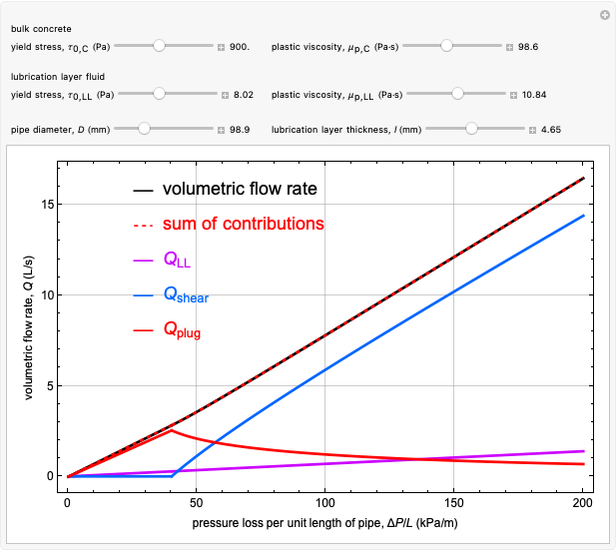
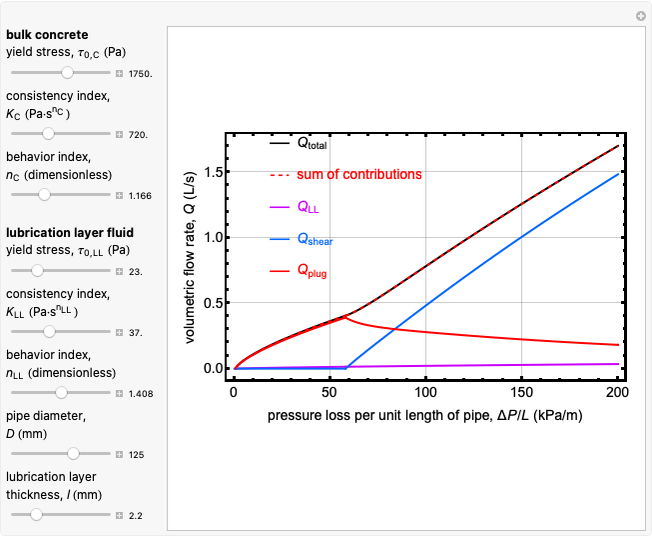
Pumping concrete is an important aspect of construction practice. This Demonstration implements a recently developed analytical model, referred to as the Khatib–Khayat model. We obtain analytical predictions of volume flow rate  versus pressure loss per unit length
versus pressure loss per unit length  , based on the two-fluid Bingham model. We predict the relation between
, based on the two-fluid Bingham model. We predict the relation between  and
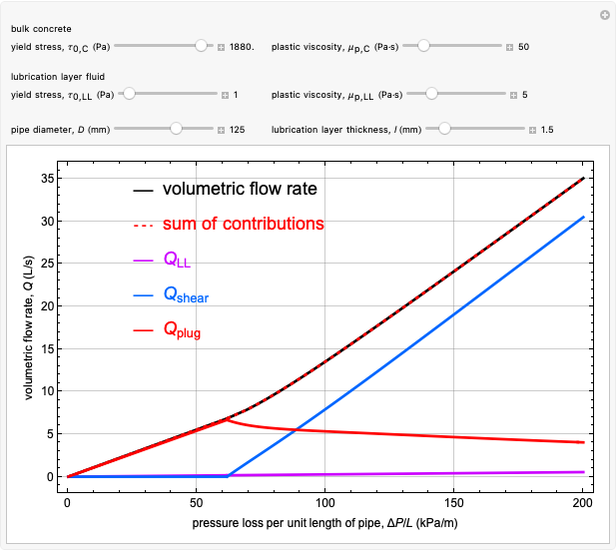
and  , given the six model parameters: two Bingham fluid parameters for the bulk concrete, two Bingham fluid parameters for the LL fluid, the pipe diameter and the lubrication layer thickness. In addition to showing the total volume flow rate, we show the three contributions to the overall volume flow rate: from the LL region, from the shearing flow region of the bulk concrete and from the plug-flow region of the bulk concrete. The sum of the three contributions is also shown, to compare with observed results for the volumetric flow rate.
, given the six model parameters: two Bingham fluid parameters for the bulk concrete, two Bingham fluid parameters for the LL fluid, the pipe diameter and the lubrication layer thickness. In addition to showing the total volume flow rate, we show the three contributions to the overall volume flow rate: from the LL region, from the shearing flow region of the bulk concrete and from the plug-flow region of the bulk concrete. The sum of the three contributions is also shown, to compare with observed results for the volumetric flow rate.
Contributed by: Balnur Zhaidarbek and Yanwei Wang (June 13)
(Nazarbayev University)
Open content licensed under CC BY-NC-SA
Details
The original model, developed by Rami Khatib and Kamal H. Khayat [1], assumed that the bulk concrete has a sufficiently low yield stress that there is always a shearing flow region in the bulk concrete. This is the case for self-compacting concrete (SCC) [2, 3]. This Demonstration extends the original Khatib–Khayat model to include pumping conventional vibrated concrete (CVC), in which the entire bulk concrete may experience only plug flow [2, 3]. The key idea behind the Khatib–Khayat model is that pumping of concrete is described by the viscoplastic Hagen–Poiseuille flow of two coaxial, immiscible, incompressible Bingham fluids, one for the bulk concrete and the other for the fluid in the lubrication layer (LL) region.
References
[1] R. Khatib and K. H. Khayat, "Pumping of Flowable Concrete: Analytical Prediction and Experimental Validation," Materials Journal, 118(5), 2021 pp. 3–16. doi:10.14359/51732928.
[2] D. Feys, "13 - Understanding the Pumping of Conventional Vibrated and Self-Compacting Concrete," Understanding the Rheology of Concrete (N. Roussel, ed.), Woodhead Publishing, 2012 pp. 331–353. doi:10.1533/9780857095282.3.331.
[3] D. Kaplan, F. de Larrard and T. Sedran, "Design of Concrete Pumping Circuit," Materials Journal, 102(2), 2005 pp. 110–117. doi:10.14359/14304.
Snapshots
Permanent Citation