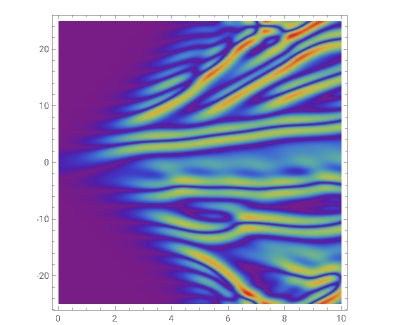
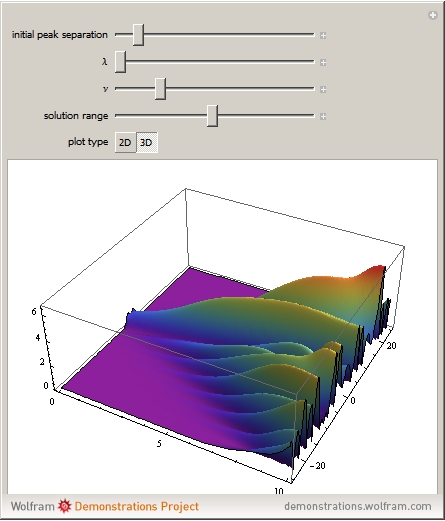
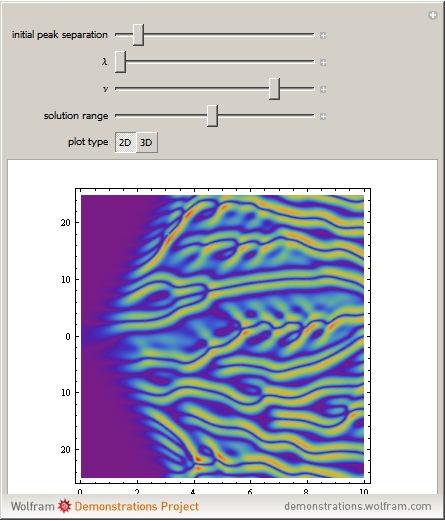
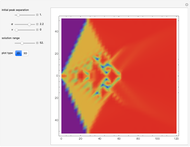
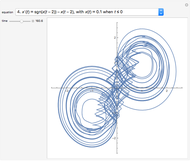
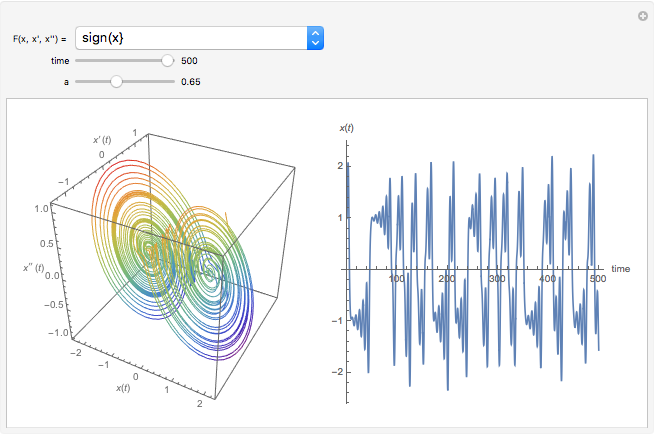
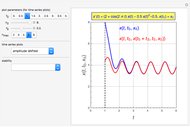
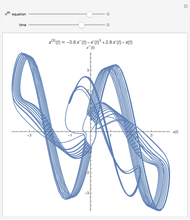
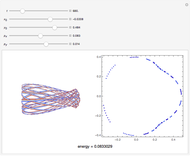
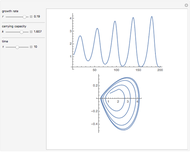
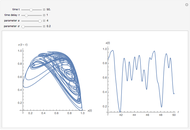
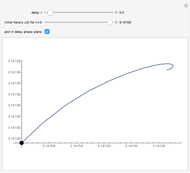
The Kuramoto–Sivashinsky equation is a nonlinear PDE that has been used as a model for complex spatiotemporal dynamics in extended systems driven far from equilibrium by intrinsic instabilities. As can be expected, the solutions of the equation exhibit chaotic behavior. The equation has been applied to model instabilities on laminar flame fronts, phase turbulence in chemical oscillations, and phase dynamics in reaction-diffusion systems, among several other applications. You can vary the dimensionless parameters and , as well as the peak separation and solution range.