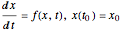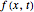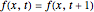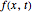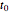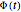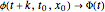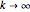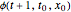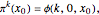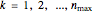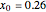Solution and Stability of a 1-Periodic Differential Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
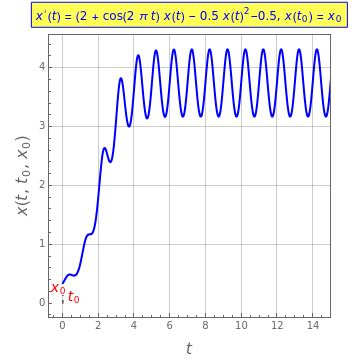
Consider an equation of the form
[more]
Contributed by: Brian G. Higgins and Housam Binous (January 2013)
Open content licensed under CC BY-NC-SA
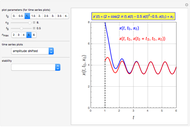
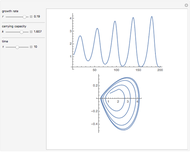
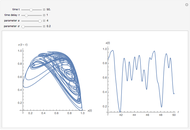
Snapshots
Details
The example used in this Demonstration is adapted from [1].
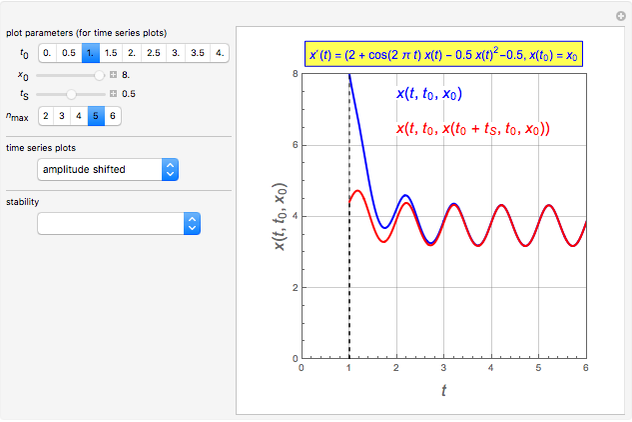
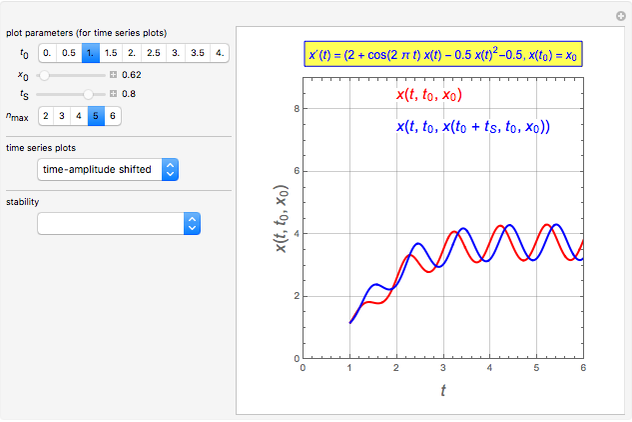
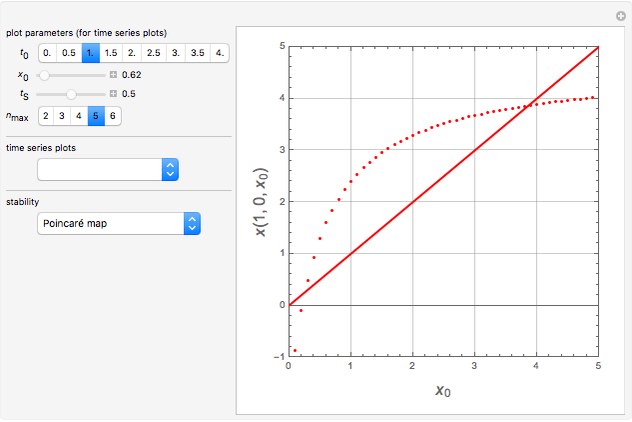
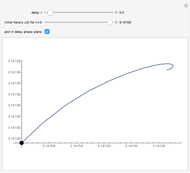
The idea of a Poincaré map is to take an arbitrary initial value 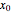 at
at  and map it to the value of the solution
and map it to the value of the solution 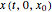 at
at  , which is
, which is 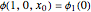 . We represent the map as
. We represent the map as
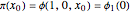 .
.
Then the 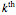 iterate of the map is given by
iterate of the map is given by
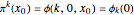 .
.
The intersection of 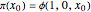 with
with  defines the fixed points of the Poincaré map. The fixed points (periodic solutions) of the Poincaré map are solutions to
defines the fixed points of the Poincaré map. The fixed points (periodic solutions) of the Poincaré map are solutions to
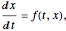
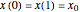 .
.
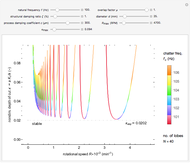
The stability of a fixed point is found by determining the Floquet exponents (using Floquet theory):
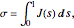
 .
.
Reference
[1] J. H. Hubbard and B. H. West, Differential Equations: A Dynamical Systems Approach, New York: Springer, 1991.
Permanent Citation