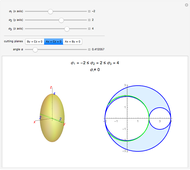
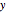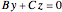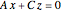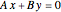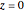Lamé's Ellipsoid and Mohr's Circles (Part 3: Meridians)

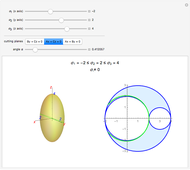
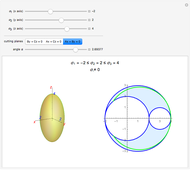
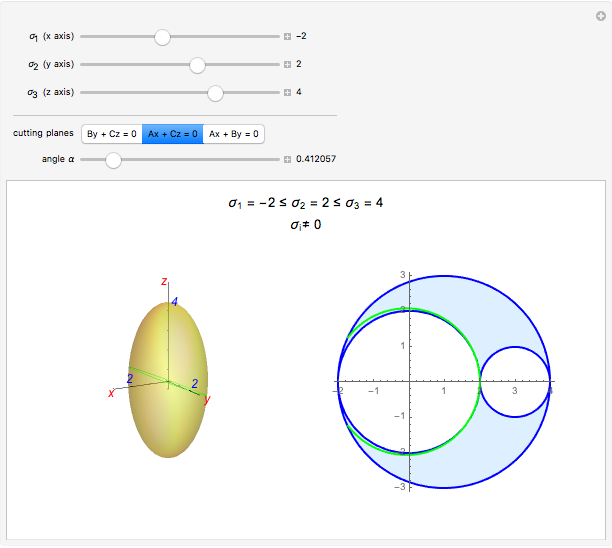
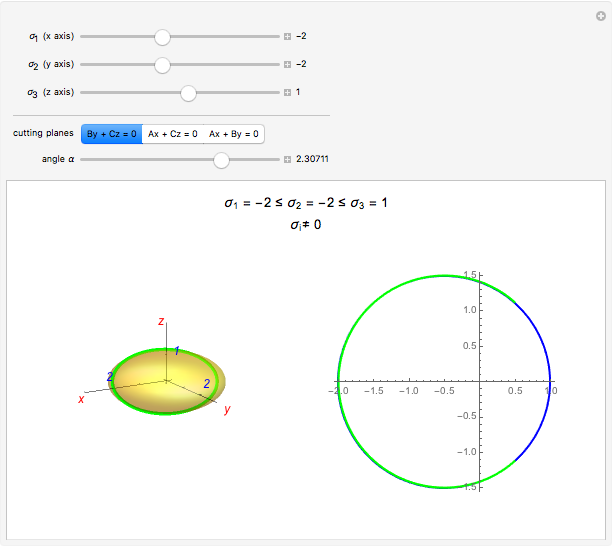
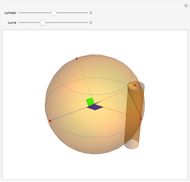
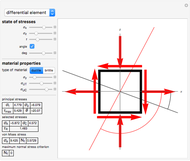
For a continuous body, the stress tensor is a symmetric matrix representing the stresses at a point. The traction vector on a plane defined by its unit normal vector 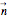is the matrix product of the stress tensor with 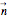. The stress tensor has three real eigenvalues (the principal stresses, 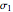, , and 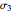) and three associated eigenvectors (the principal directions). In the coordinate system defined by these eigenvectors, the Lamé's ellipsoid represents the locus of the traction vector heads.

This Demonstration shows ellipses, called meridians, obtained by cutting Lamé's ellipsoid by sheaves of planes through the , , and axes, with equations

,

,

.

In the first two cases, is the angle between the plane and the - plane (); in the third case is the angle between the plane and the - plane ().

The points of the meridians are endpoints of the traction vectors, whose intrinsic components (normal and tangential) are represented by green loci within the Mohr circles.