Lamé's Ellipsoid and Mohr's Circles (Part 4: Spheres)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
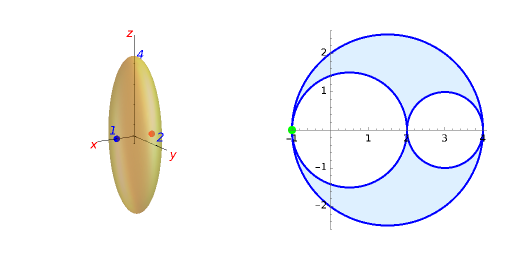
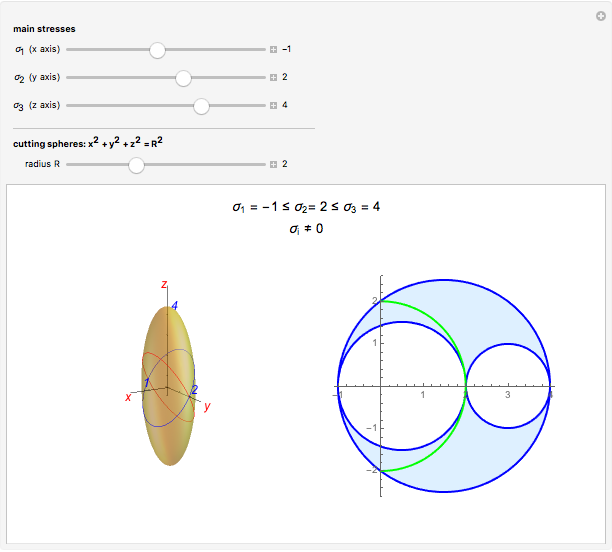
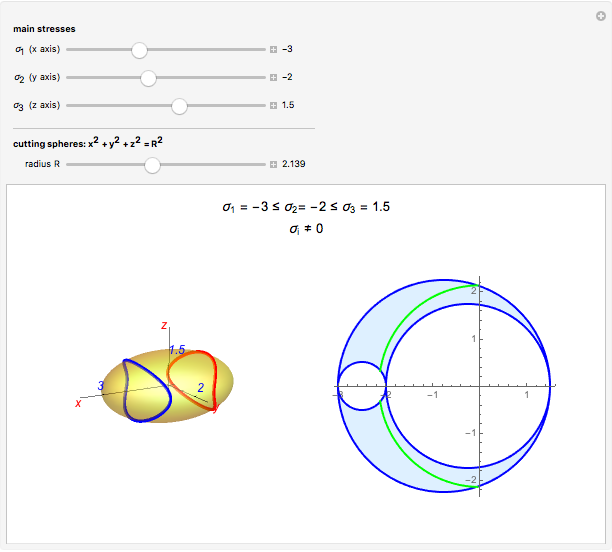
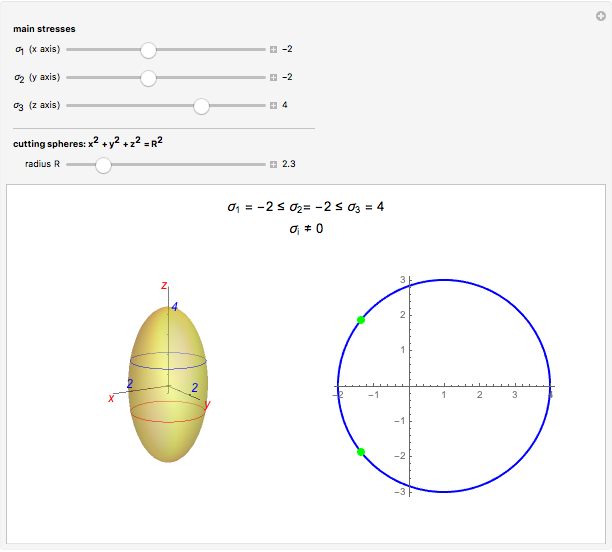
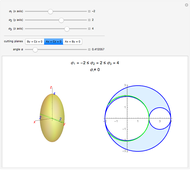
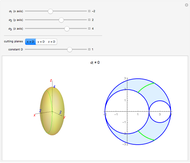
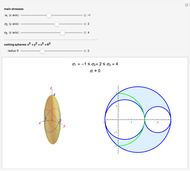
Given a continuum body, the stress tensor is a symmetric matrix that contains the stresses at a point. The traction vector on a plane defined by its perpendicular unitary vector,  , is obtained multiplying the stress tensor by
, is obtained multiplying the stress tensor by  . The stress tensor has three real eigenvalues (the principal stresses:
. The stress tensor has three real eigenvalues (the principal stresses:  ,
,  , and
, and  ) and three associated eigenvectors (the principal directions). On the coordinate system defined by these eigenvectors Lamé's ellipsoid represents where the heads of the traction vectors lie.
) and three associated eigenvectors (the principal directions). On the coordinate system defined by these eigenvectors Lamé's ellipsoid represents where the heads of the traction vectors lie.
Contributed by: Luis Martín Yagüe, Agustín Lacort Echeverría, and Antonio Sánchez Parandiet (March 2011)
After work by: Eugenio Bravo Sevilla
Open content licensed under CC BY-NC-SA
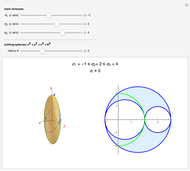
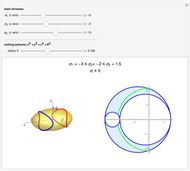
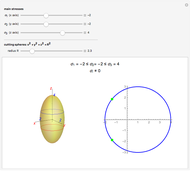
Snapshots
Details
detailSectionParagraphPermanent Citation
"Lamé's Ellipsoid and Mohr's Circles (Part 4: Spheres)"
http://demonstrations.wolfram.com/LamesEllipsoidAndMohrsCirclesPart4Spheres/
Wolfram Demonstrations Project
Published: March 7 2011