Liénard-Wiechert Potential for Spiraling Charge

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
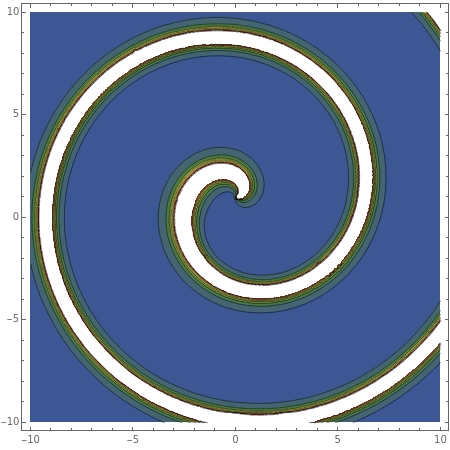
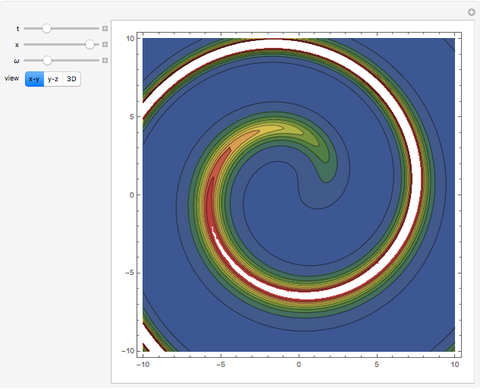
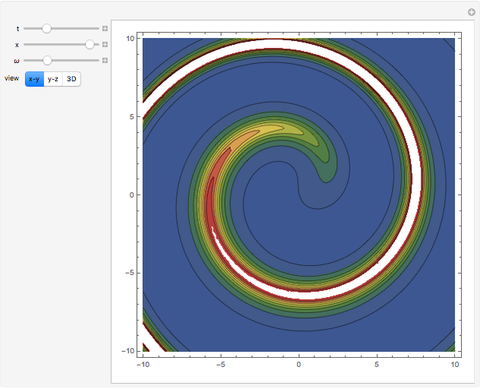
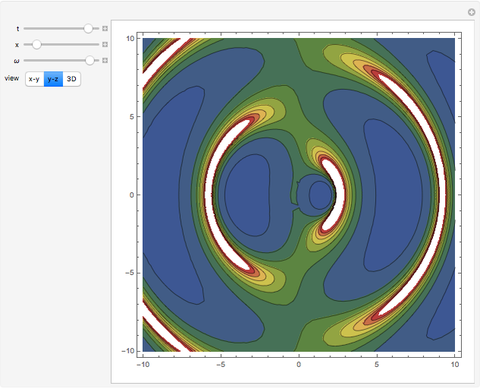
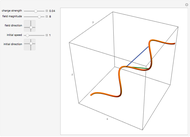
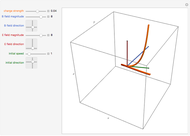
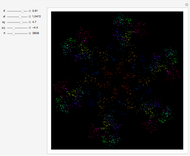
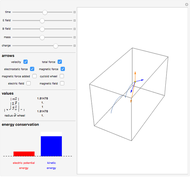
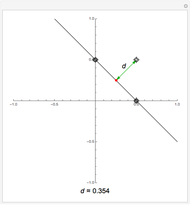
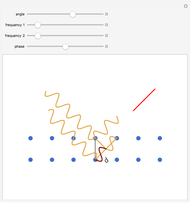
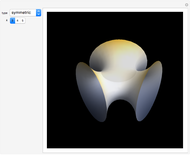
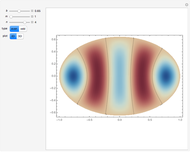
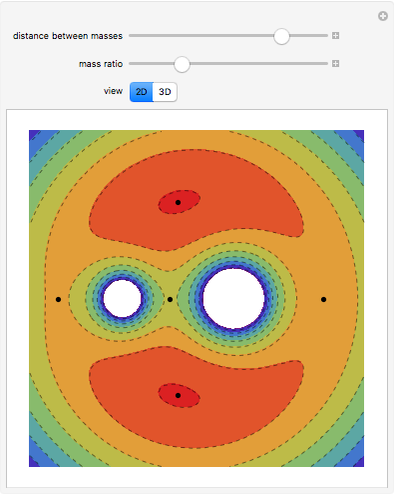
The graphics show different views of the radiation patterns produced by a point charge moving in an inward spiral trajectory with angular velocity  . Since a charge moving in a circular orbit is continually undergoing centripetal acceleration
. Since a charge moving in a circular orbit is continually undergoing centripetal acceleration  , it radiates away energy in accordance with Larmor's formula
, it radiates away energy in accordance with Larmor's formula  (in Gaussian units). As energy is lost, the radius decreases as the charge spirals inward toward the attracting center. Neglecting any contribution from the radiation field, the Liénard–Wiechert scalar potential
(in Gaussian units). As energy is lost, the radius decreases as the charge spirals inward toward the attracting center. Neglecting any contribution from the radiation field, the Liénard–Wiechert scalar potential  produced by the moving charge is computed. This treatment is valid for
produced by the moving charge is computed. This treatment is valid for  , and thus excludes the ultrarelativistic domain.
, and thus excludes the ultrarelativistic domain.
Contributed by: Enrique Zeleny (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
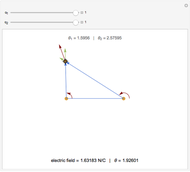
The Liénard–Wiechert scalar potential is given by  where
where  is the electron charge,
is the electron charge,  is the velocity vector, and
is the velocity vector, and  is the distance from the current position
is the distance from the current position  to the original position
to the original position  at the retarded time
at the retarded time  . The last equation is solved iteratively, updating the direction of the field from the charge's instantaneous position. As mentioned in the Caption, the computation is valid provided that
. The last equation is solved iteratively, updating the direction of the field from the charge's instantaneous position. As mentioned in the Caption, the computation is valid provided that  .
.
References
[1] M. Trott, The Mathematica Guidebook for Graphics, New York: Springer-Verlag, 2004.
[2] K. Kokkotas. "Radiation by Moving Charges." (May 9, 2010) www.tat.physik.uni-tuebingen.de/~kokkotas/Teaching/Field_Theory_files/FT_course05.pdf.
Permanent Citation