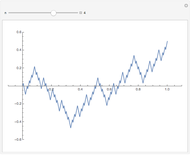
Sine Wave Example of the Epsilon-Delta Definition of Limit

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
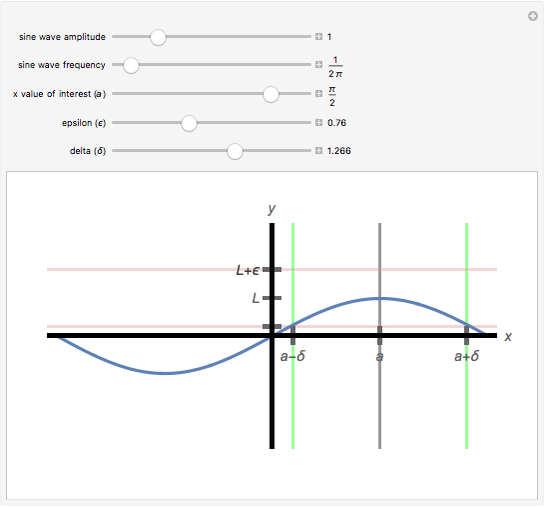
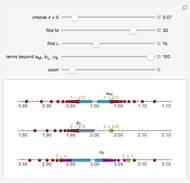
This Demonstration illustrates the  -
- definition for the limit
definition for the limit  of the sinusoid
of the sinusoid  as
as  tends to
tends to  . You can vary the amplitude
. You can vary the amplitude  , the frequency
, the frequency  , and the
, and the  value of interest,
value of interest,  . Then, for each chosen value for
. Then, for each chosen value for  , you can find a valid
, you can find a valid  , i.e., a
, i.e., a  such that whenever
such that whenever  ,
,  . When a valid
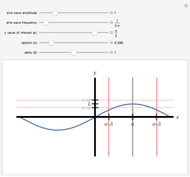
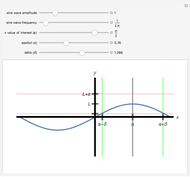
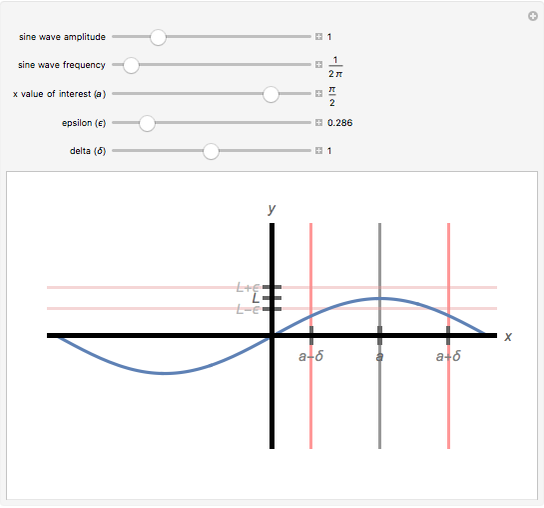
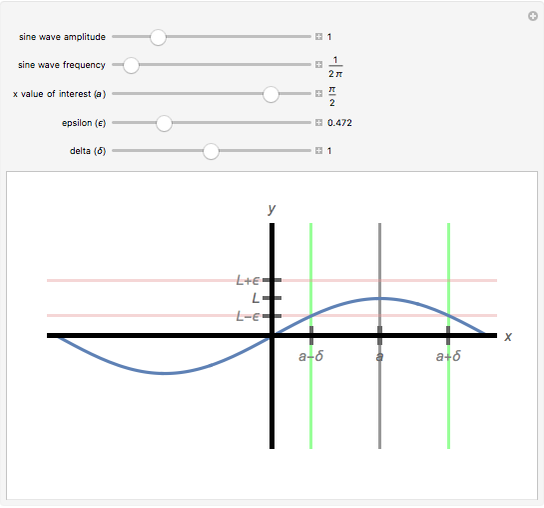
. When a valid  has been found, the vertical sides of the
has been found, the vertical sides of the  box appear green. For an invalid
box appear green. For an invalid  , the vertical sides of the
, the vertical sides of the  box appear red.
box appear red.
Contributed by: Geoffrey F. Miller, Daniel C. Cheshire, Nell H. Wackwitz, Joshua B. Fagan (May 2015)
(Texas State University)
Based on a program by: Joseph F. Kolacinski
Open content licensed under CC BY-NC-SA
Snapshots
Details
The sine function is very important in mathematics and physics. The sine function can also serve as a great example to demonstrate the  -
- definition of the limit of a function.
definition of the limit of a function.
Recall that a function 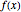 has limit
has limit  at
at  provided that for every
provided that for every  , there is a
, there is a  such that
such that  whenever
whenever  . This gives rise to the concept of an
. This gives rise to the concept of an  box (or
box (or  window or
window or  rectangle).
rectangle).
The vertical sides of the  box turn green for an appropriate choice of
box turn green for an appropriate choice of  and are red otherwise. Changing the sine wave's amplitude, frequency, and the
and are red otherwise. Changing the sine wave's amplitude, frequency, and the  value of interest affects the valid choices of
value of interest affects the valid choices of  . For a valid choice of
. For a valid choice of  , the sine wave does not cross over the bottom or the top of the
, the sine wave does not cross over the bottom or the top of the  box.
box.
Permanent Citation