Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Lorenz's Water Wheel

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

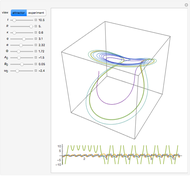
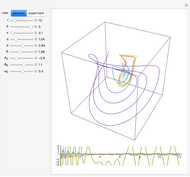
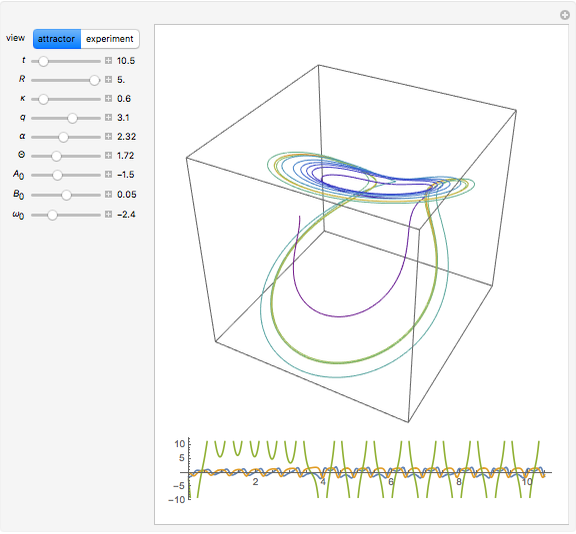
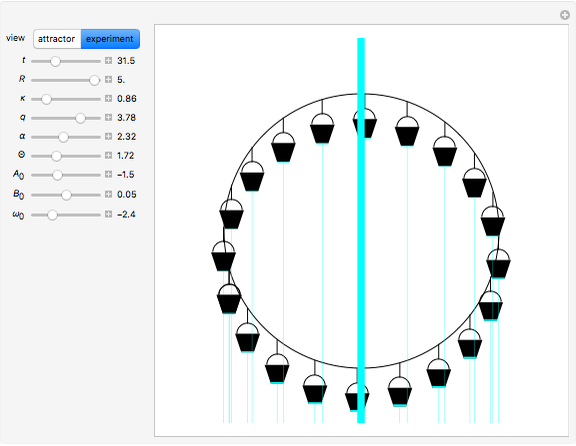
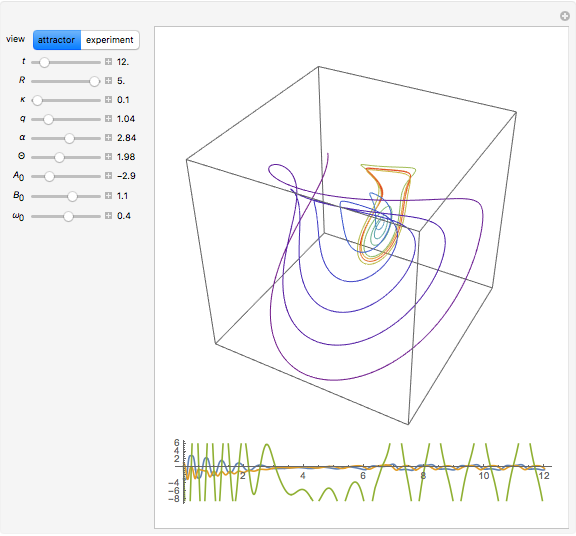
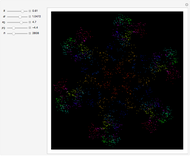
In Lorenz's water wheel, equally spaced buckets hang in a circular array. Water pours into the top bucket and leaks out of each bucket at a fixed rate. The wheel behaves chaotically for certain choices of parameters, showing unpredictable changes in the direction of rotation. This behavior of this system is analogous to that of a Lorenz attractor.

Contributed by: Enrique Zeleny (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The equations of motion are:

where:

is the radius of the wheel is the leakage rate is the flow rate into the top bucket is the rotational damping rate is the moment of inertia of the wheel is gravitational acceleration

The system is modeled as a ring; by assumption, the amount of water in a section (represented by a bucket) of the ring is proportional to , where is the angle of the bucket moving with angular velocity for initial conditions , , and .

Reference

[1] T. Tél and M. Gruiz, Chaotic Dynamics, An Introduction Based on Classical Mechanics, New York: Cambridge University Press, 2006.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send