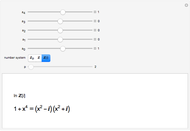Mandelbrot's Binomial Measure Multifractal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
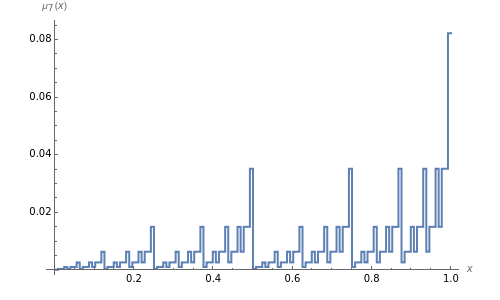
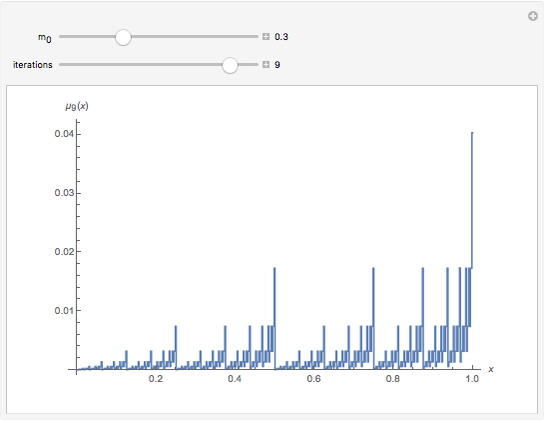
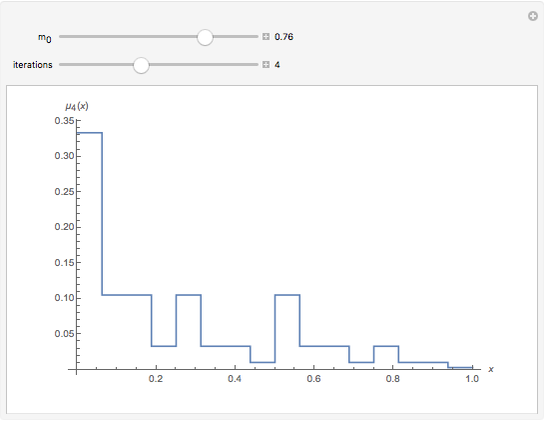
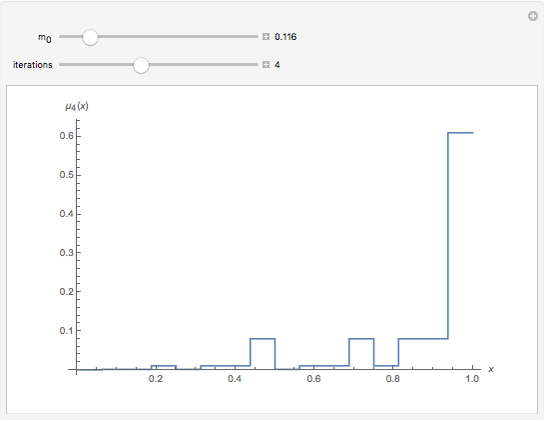
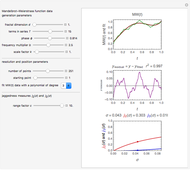
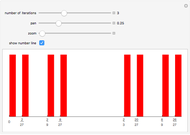
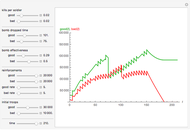
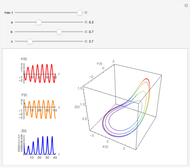
This Demonstration illustrates the simplest multifractal: Mandelbrot's binomial measure on the interval  . The iteration begins with a uniform distribution
. The iteration begins with a uniform distribution  (with
(with  ), subdivides it into a distribution with
), subdivides it into a distribution with  and
and  , further subdivides it into
, further subdivides it into  ,
,  ,
,  , and
, and  , and so on. Additional iteration of this procedure gives a multiplicative cascade that generates an infinite sequence of measures; the limit of the measures is the binomial measure.
, and so on. Additional iteration of this procedure gives a multiplicative cascade that generates an infinite sequence of measures; the limit of the measures is the binomial measure.
Contributed by: Eric W. Weisstein (March 2011)
Open content licensed under CC BY-NC-SA
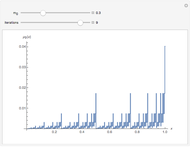
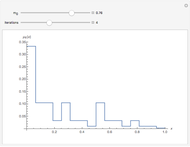
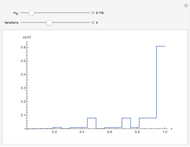
Snapshots
Details
B. B. Mandelbrot, "Intermittent Turbulence in Self Similar Cascades: Divergences of High Moments and Dimension of the Carrier," Journal of Fluid Mechanics, 62, 1974 pp. 331–365. B. B. Mandelbrot, et al. "A Multifractal Model of Asset Returns". (1997).
S. Seuret and J. L. Véhel, "The Local Hölder Function of a Continuous Function," Computational Harmonic Analysis, 13(3), 2002 pp. 263–276.
Permanent Citation
"Mandelbrot's Binomial Measure Multifractal"
http://demonstrations.wolfram.com/MandelbrotsBinomialMeasureMultifractal/
Wolfram Demonstrations Project
Published: March 7 2011