Population Sizes and Interactions during the Zombie Apocalypse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
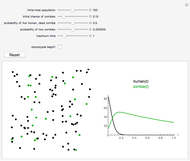
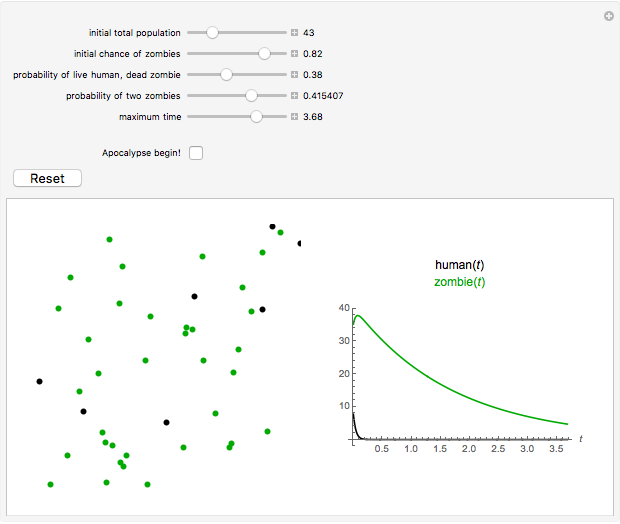
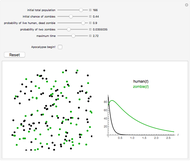
This Demonstration models the spread of the zombie pathogen during a potential apocalyptic scenario. Zombies are portrayed as green dots, while the humans are black dots that become green as they are infected. You can alter the probability that a human survives and the probability that a zombie successfully infects a human. This scenario, while highly implausible, nonetheless provides insight into a unique model of infection, in which the projected infection rate is visualized using both a predator/prey model and the corresponding Lotka–Volterra equations to plot changes in both populations.
Contributed by: Soumik Biswas and Renata Wettermann (June 2013)
Based on programs by Eric W. Weisstein and Hiroki Sayama
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: In this scenario, before the apocalypse begins, the ratio of zombies to humans can be observed; it has been influenced by a medium-high "initial chance of zombies".
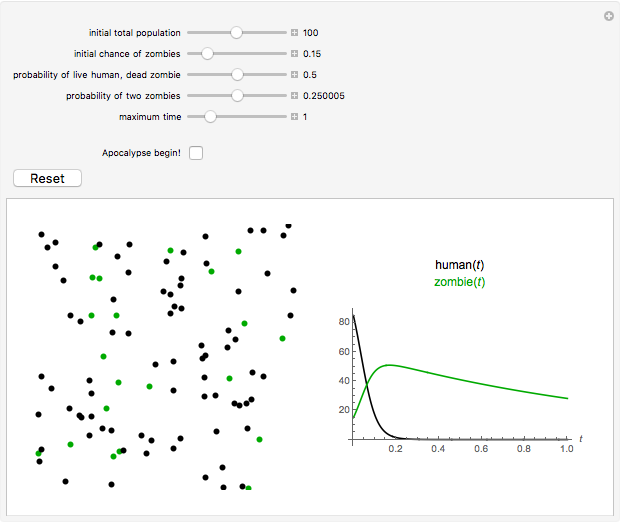
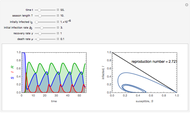
Snapshot 2: Here, the high initial likelihood of zombies and the greater probability of two zombies than that of a live human and dead zombie have contributed to near-total destruction of the human race. The population graphs correspond accordingly, with the human population (black) decreasing to zero as the zombie population (green) exhibits a more gradual slope, indicative of the lesser rate of population loss.
Snapshot 3: Adjusting the "maximum time" slider would show a projection of zombie and human populations over time, taking into account the selected probabilities of zombie-human interactions.
Users may use the sliders to alter the probability of two scenarios: 1. Zombies can successfully infect humans with the pathogen, creating another zombie. 2. Humans can successfully kill a zombie without being infected.
Altering these factors will indirectly alter the probability of a third scenario: 3. Both a human and a zombie are killed during a skirmish.
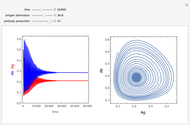
The effects of altering these probabilities in turn alter both the zombie and human populations. This Demonstration includes a straightforward visual representation of the scenario at hand, in which individual humans and zombies are represented as dots that are in random motion. Additionally, the population is represented graphically using the Lotka–Volterra equations for predator-prey interactions. In altering the probability of each scenario, the constants associated with the Lotka–Volterra differential equations change accordingly, altering the population size with respect to time. Using the sliders for altering initial population size and the maximum time will allow users to understand specific scenarios that are associated with the given parameters for population growth and decay. The constant A (the growth rate of humans) is assumed to be 0 in this model. B (the rate at which zombies destroy humans) is proportional to the probability of Scenario 1 + Scenario 3. C (the death rate of zombies) is proportional to the probability of Scenarios 2 and 3, and D (the rate at which zombies increase by consuming humans) is proportional to the probability of Scenario 1.
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School.
References
[1] A. S. Khan, "Preparedness 101: Zombie Apocalypse," Centers for Disease Control and Prevention: Public Health Matters Blog (blog). (May 16, 2011) blogs.cdc.gov/publichealthmatters/2011/05/preparedness-101-zombie-apocalypse.
[2] Michael Jackson - Thriller. [Video] (Oct 2, 2009) www.youtube.com/watch?v=sOnqjkJTMaA.
[3] University of Michigan. "Trophic Links: Predation and Parasitism." (Nov 2, 2005) www.globalchange.umich.edu/globalchange1/current/lectures/predation/predation.html.
[4] Wikipedia. "Lotka–Volterra Equation." (Apr 18, 2013) en.wikipedia.org/wiki/Lotka% E2 %80 %93 Volterra_equation.