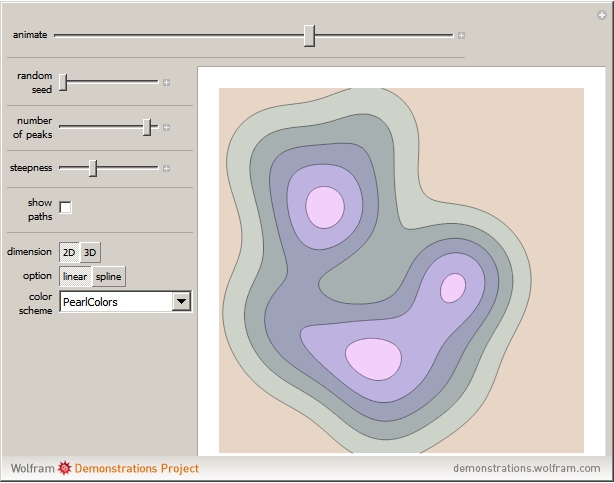
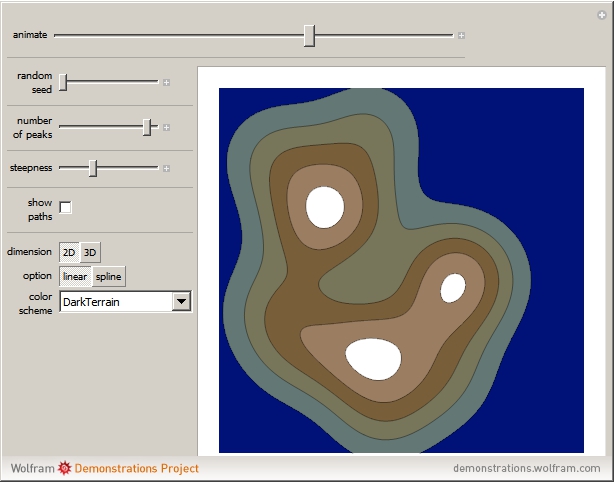
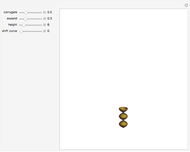
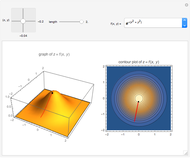
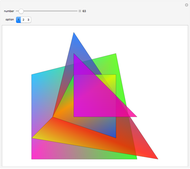
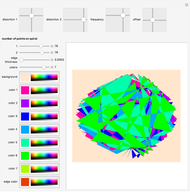
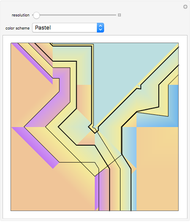
A set of points is selected parametrically from either a set of randomly generated line segments or from a randomly generated set of closed B-spline paths. Each point is the tip of a three-dimensional Gaussian curve that appears as a mountain. The mountains merge together and separate as the points follow their paths. You can view the mountains either as a 3D plot or as a 2D contour map. When viewed as a contour map, you can show the paths superimposed over it. You can modify the steepness of the mountains in relation to the diameter of its base with the "steepness" slider. Setting the top slider to play gives interesting animations.