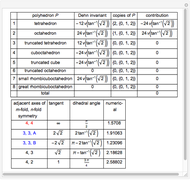
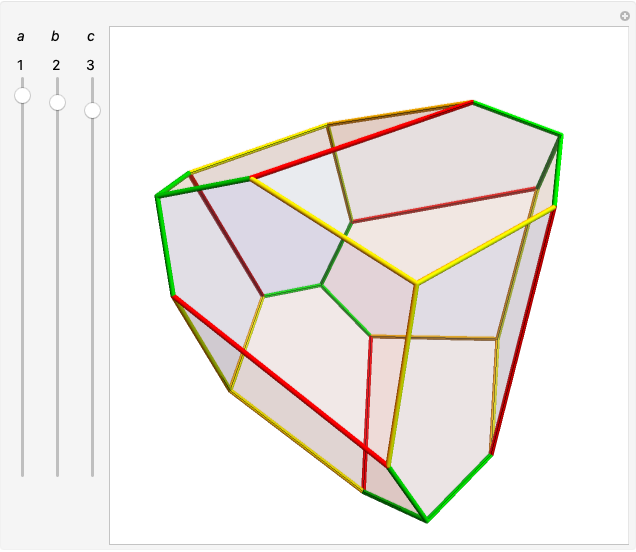
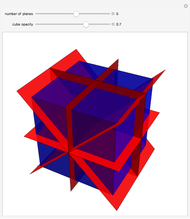
Mirror Symmetries of the Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
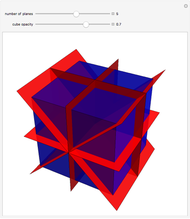
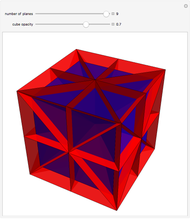
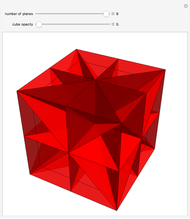
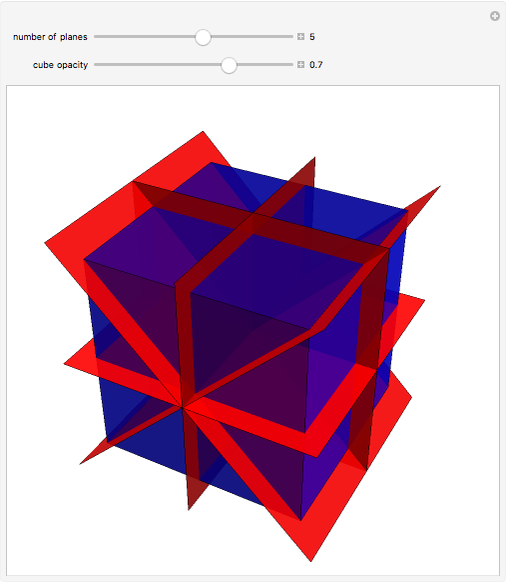
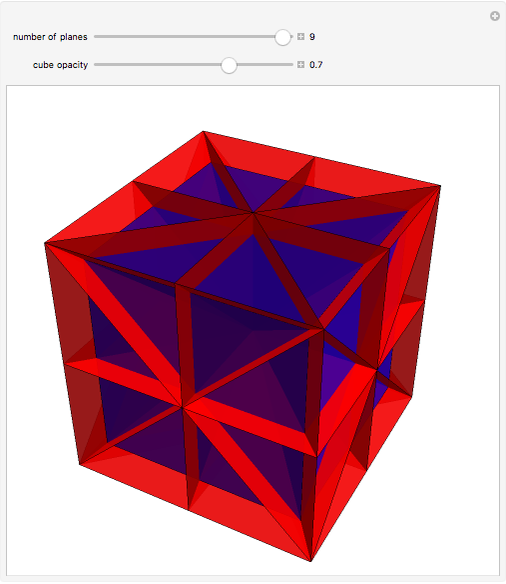
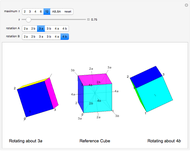
Use the slider to show the nine planes of symmetry (or mirror planes) for the cube. If the center of the cube is the origin  and the
and the  ,
, 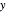 , and
, and  axes are normal to opposite pairs of faces, the planes have equations
axes are normal to opposite pairs of faces, the planes have equations  ,
,  ,
, 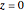 ,
, 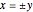 ,
, 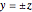 , and
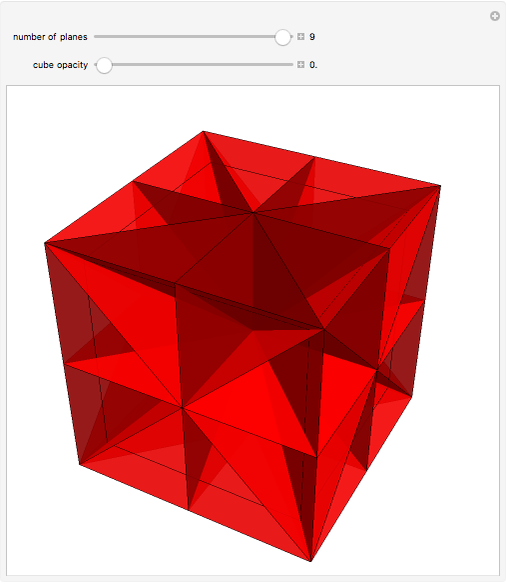
, and 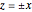 . With all nine cuts, each of the six faces of the cube is cut into eight triangles. For each such triangle, join its three vertices to the center of the cube to form a tetrahedron. These 48 tetrahedra partition the cube. (Reduce the opacity to see their interiors.)
. With all nine cuts, each of the six faces of the cube is cut into eight triangles. For each such triangle, join its three vertices to the center of the cube to form a tetrahedron. These 48 tetrahedra partition the cube. (Reduce the opacity to see their interiors.)
Contributed by: Aaron Wallace (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Mirror Symmetries of the Cube"
http://demonstrations.wolfram.com/MirrorSymmetriesOfTheCube/
Wolfram Demonstrations Project
Published: November 23 2015