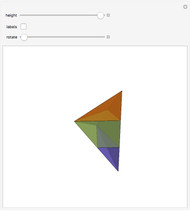
Cubic Symmetry Types

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
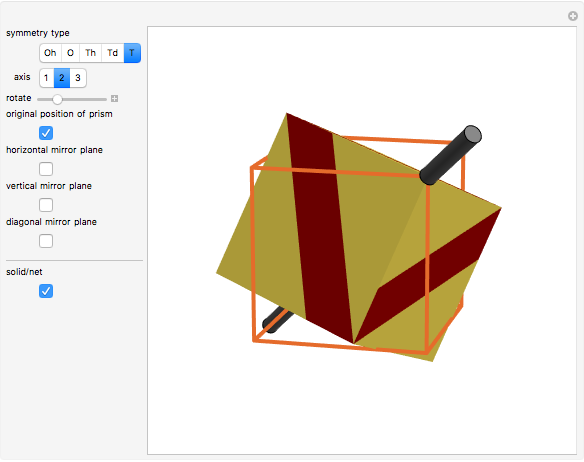
This Demonstration illustrates cubic symmetry types.
Contributed by: Izidor Hafner (May 2008)
Based on work by: Peter R. Cromwell
Open content licensed under CC BY-NC-SA
Snapshots
Details
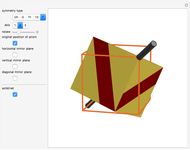
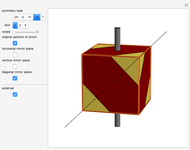
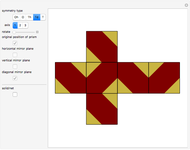
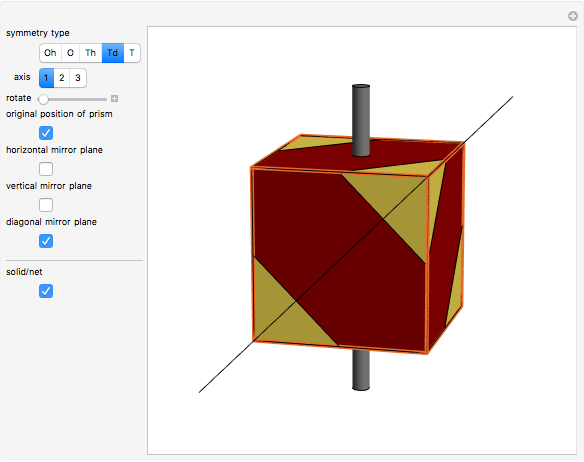
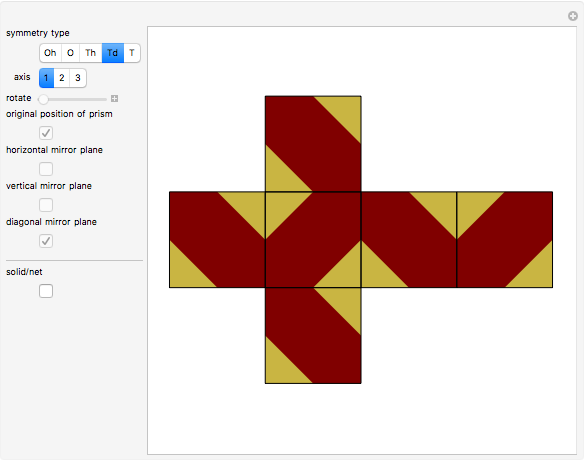
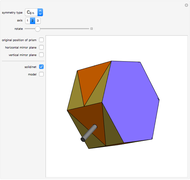
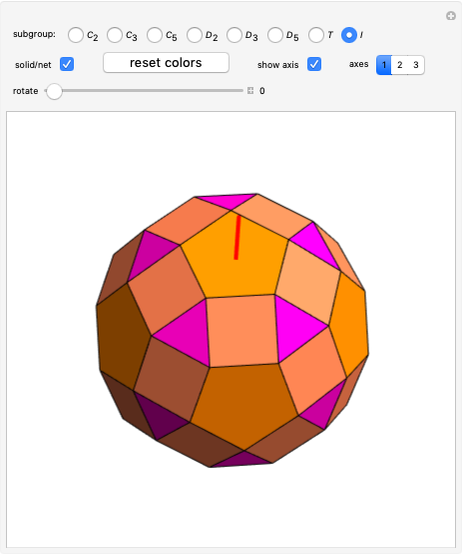
A polyhedron with cubic symmetry has the same axes of rotational symmetry as a cube (or an octahedron, so the system is labeled 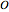 ) or an axis of four-fold symmetry is reduced to a two-fold axis and the result is a tetrahedral system of rotational symmetry (labeled
) or an axis of four-fold symmetry is reduced to a two-fold axis and the result is a tetrahedral system of rotational symmetry (labeled  ). If the polyhedron is placed so that an axis of four-fold symmetry points vertically and there is a horizontal reflection plane, the system of symmetry has label
). If the polyhedron is placed so that an axis of four-fold symmetry points vertically and there is a horizontal reflection plane, the system of symmetry has label 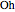 . If all reflection symmetries are destroyed, the system of symmetry has label
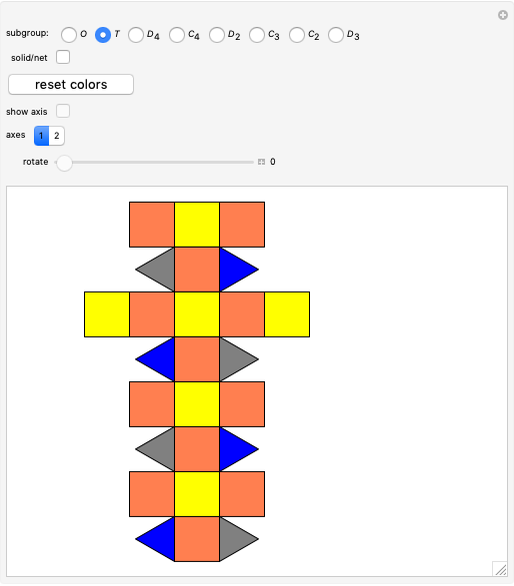
. If all reflection symmetries are destroyed, the system of symmetry has label 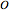 . If a polyhedron is decorated so that four-fold axes are changed to two-fold axes and there is a horizontal reflection plane, the system is labeled
. If a polyhedron is decorated so that four-fold axes are changed to two-fold axes and there is a horizontal reflection plane, the system is labeled 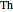 . If there is no horizontal reflection plane (and as a consequence, there are no vertical reflection planes), but there are reflection planes that contain axes of three-fold symmetry, the system of symmetry is labeled
. If there is no horizontal reflection plane (and as a consequence, there are no vertical reflection planes), but there are reflection planes that contain axes of three-fold symmetry, the system of symmetry is labeled 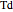 . If all reflection symmetries are destroyed, the system is labeled
. If all reflection symmetries are destroyed, the system is labeled 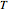 .
.
Reference
[1] P. R. Cromwell, Polyhedra, New York: Cambridge Univ. Press, 1997 pp. 308–311.
Permanent Citation
"Cubic Symmetry Types"
http://demonstrations.wolfram.com/CubicSymmetryTypes/
Wolfram Demonstrations Project
Published: May 21 2008