More Uniform Polyhedra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
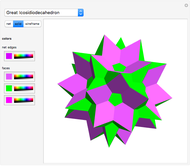
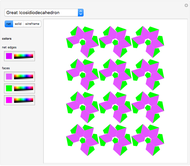
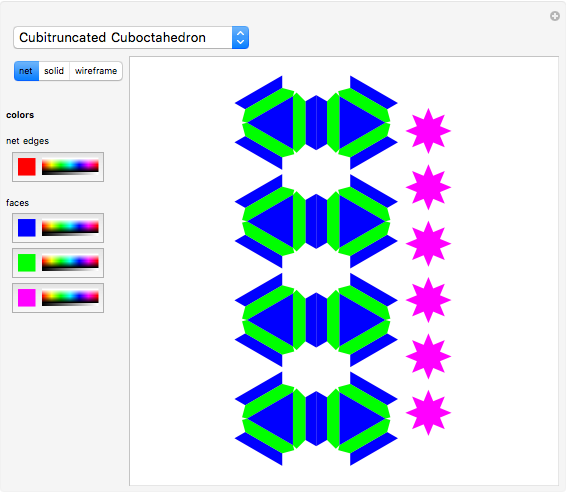
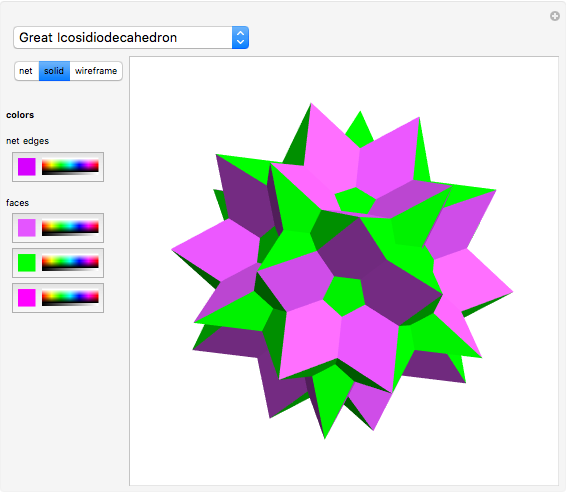
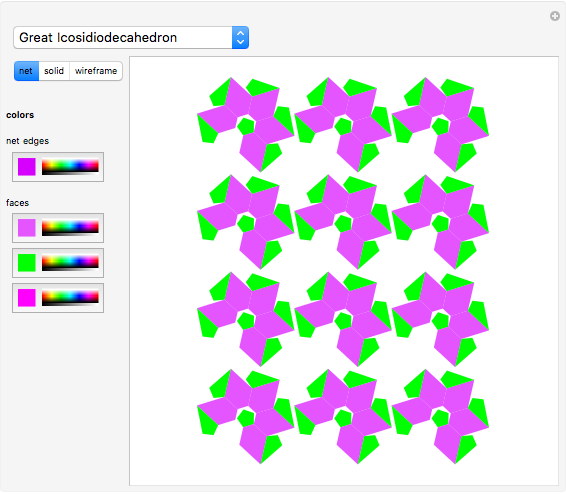
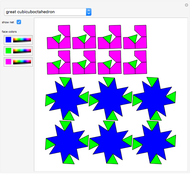
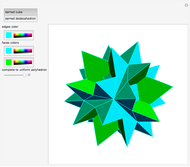
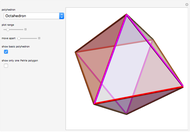
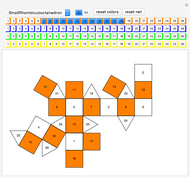
A polyhedron is uniform if all of its faces are regular polygons, and it is transitive on its vertices ("all the vertices look the same"). It is possible for the faces to intersect and for three faces to cross at a point that is not a vertex. This Demonstration shows eleven nonconvex uniform polyhedra and their nets. The wireframe shows some of the edges of the figure.
Contributed by: Izidor Hafner (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In [5], Wenninger recommends making polyhedron models as a classroom activity. Among other polyhedra he chooses 15 nonconvex uniform polyhedra. This Demonstration shows 11 of them; five are in Uniform Polyhedron (Wolfram MathWorld). He quotes Coxeter [1]: "The chief reason for studying regular polyhedra is still the same as in the time of the Pythagoreans, namely, that their symmetrical shapes appeal to one's artistic sense."
Coordinates of polyhedra were calculated using [3] and [4].
References
[1] H. S. M. Coxeter, Regular Polytopes, New York: Dover, 1973.
[2] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
[3] R. E. Maeder, The Mathematica Programmer II, San Diego: Academic Press, 1996.
[4] R. Webb. "Great Stella." (2014) www.software3d.com/Stella.php.
[5] M. J. Wenninger, Polyhedron Models for the Classroom, Reston, VA: National Council of Teachers of Mathematics, 1975.
Permanent Citation
"More Uniform Polyhedra"
http://demonstrations.wolfram.com/MoreUniformPolyhedra/
Wolfram Demonstrations Project
Published: September 8 2014