Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

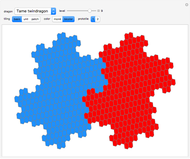
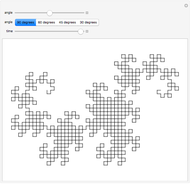
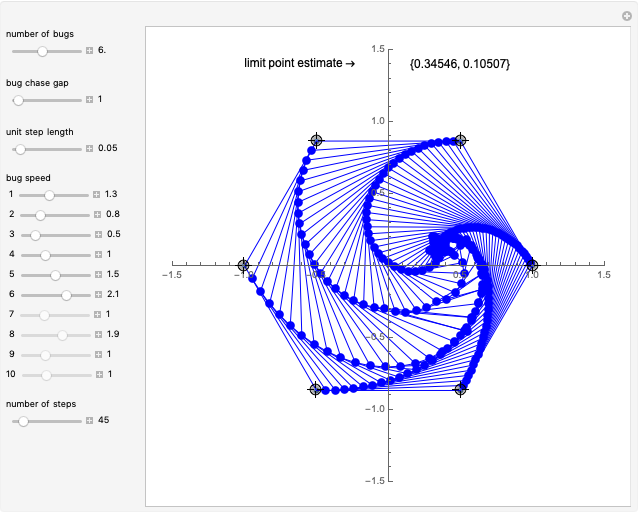
Multi-Bug Problem with Variable Speeds and Gaps

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

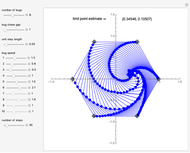
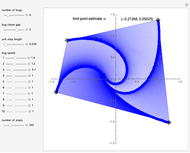
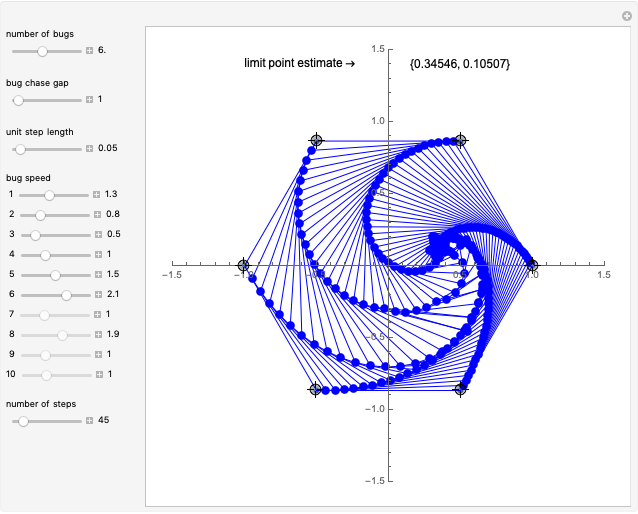
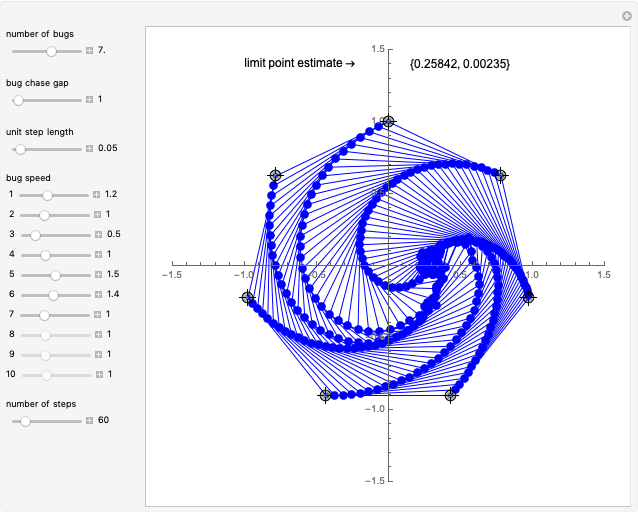
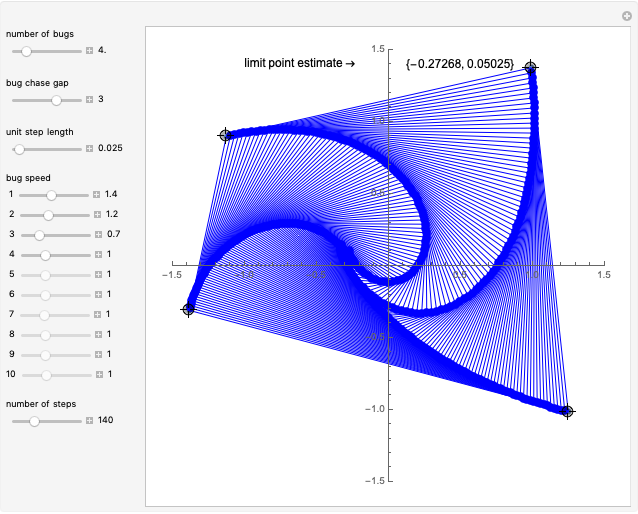
This Demonstration is an extension of a previous Demonstration by Michael Waters. It extends the four-bug problem in several ways.

[more]

Consider bugs placed regularly around the circumference of a circle. With each step, each bug takes one step closer to a counterclockwise neighbor, and a line is draw between the two.

You can vary the number of bugs, the step length and the number of steps. Also, the bugs are locators that you can drag. If you move the locators, do not change their sequential order.

The neighbor may be one or more positions away, but the gap between neighbors must be relatively prime to the number of bugs so that the sequence forms a complete cycle. Otherwise, the display will almost always revert to a gap of one. Something interesting might still happen if the values are odd.

By symmetry, it is only necessary to have the 'bug chase gap" go halfway around the circle of bugs. For example, for the 10-bug case there are only options for gaps of 1 and 3. You can also vary the speed of each bug.

When it appears that the bugs converge, the point of convergence is approximated. If the paths do not converge, then the limit point will be listed as "unavailable". The limit point is also unavailable early in the journey.

[less]

Contributed by: Carl McCarty (July 2020)
Based on: Extended Four-Bug Problem by Michael Waters
Open content licensed under CC BY-NC-SA

Snapshots

Details

Set "bug chase gap" to 1 for bugs to chase their immediate neighbor as in the classic chase problem. A value of 2 indicates the bugs skip the nearest neighbor and follow the second-closest neighbor.

The speed of a bug is the multiple of the unit step length that it takes. Thus, a value of 2 indicates that the bug is traveling twice as fast or its step is twice as long as the global step size.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send