Path of an Ant on the Diameter of a Circle Rotating on the Unit Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
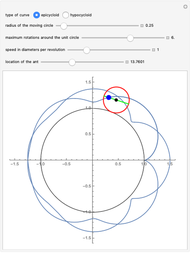
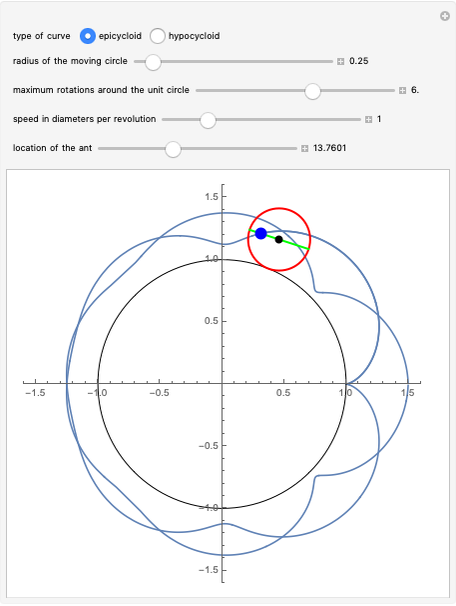
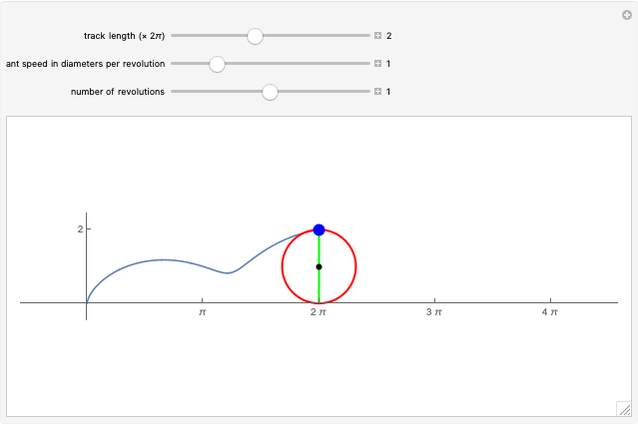
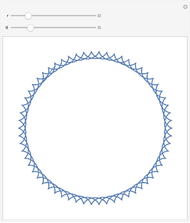
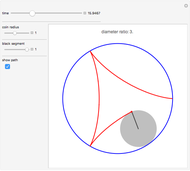
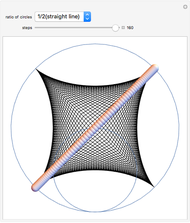
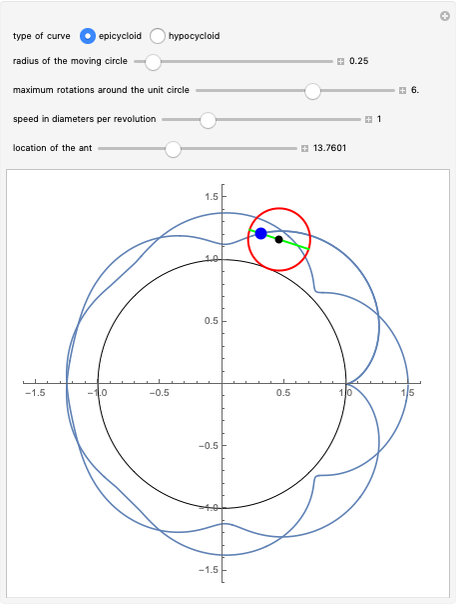
An ant, indicated by the blue dot, begins at the point (1,0) on the circumference of the red circle, which rotates at a constant speed either inside or outside the unit circle. As the circle rotates, the ant starts moving along the green diameter, also at some constant speed, until it reaches the other end. At that moment, the ant turns and immediately begins to traverse the diameter in the opposite direction. The ant repeats this action in an assigned number of circuits of the unit circle. The path of the ant is shown as the blue curve traced behind it from the point (1,0) to the blue dot.
[more]
Contributed by: Carl McCarty (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation