Multi-Time Bifurcations of Wavefronts in 2D and 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
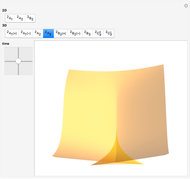
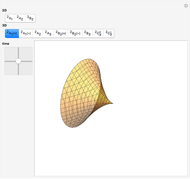
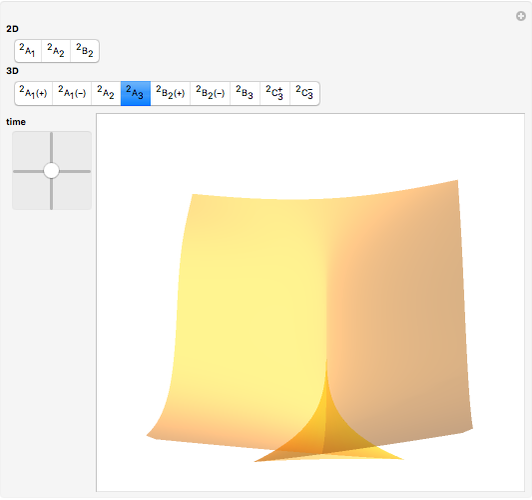
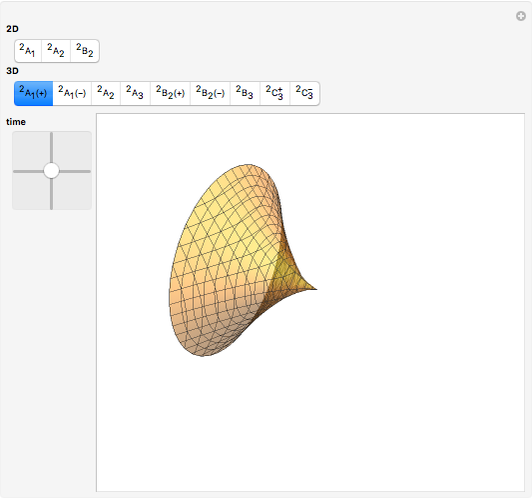
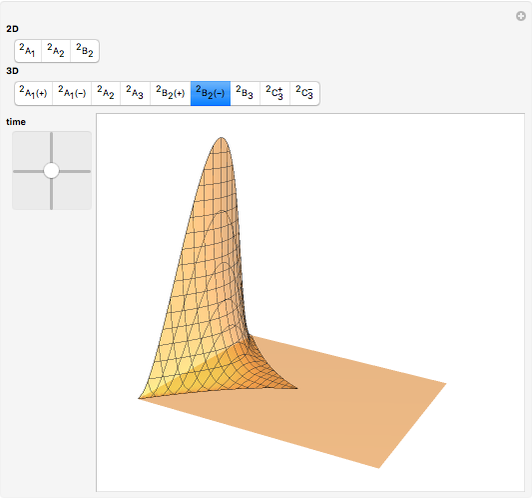
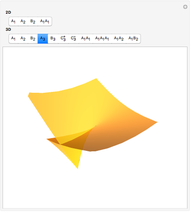
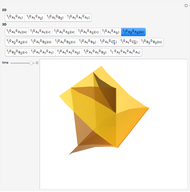
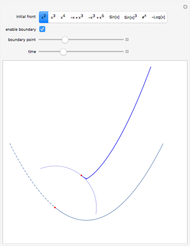
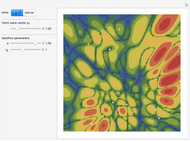
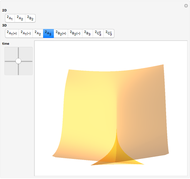
This Demonstration shows all "generic" multi-bifurcations of wavefronts in 2D and 3D. You can control the time.
Contributed by: Takaharu Tsukada (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In [5], the author constructs the theory of reticular Legendrian unfoldings that describes stable and generic multi-bifurcations of wavefronts generated by a hypersurface germ with a boundary, a corner, or an  ‐corner.
‐corner.
In the case 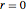 , the hypersurface has no boundary; a two-parameter family of wavefronts
, the hypersurface has no boundary; a two-parameter family of wavefronts 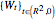 is given by a generating family
is given by a generating family 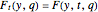 defined on
defined on 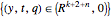 such that
such that
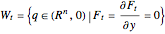 .
.
In the case 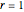 , the hypersurface has a boundary; a reticular Legendrian unfolding gives the wavefront
, the hypersurface has a boundary; a reticular Legendrian unfolding gives the wavefront 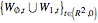 , where the set
, where the set 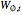 is the wavefront generated by the hypersurface at time
is the wavefront generated by the hypersurface at time  , and the set
, and the set  is the wavefront generated by the boundary of the hypersurface at time
is the wavefront generated by the boundary of the hypersurface at time  .
.
A reticular Legendrian unfolding has a generating family. Then the wavefront 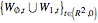 is given by the generating family
is given by the generating family 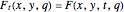 defined on
defined on 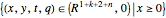 such that
such that
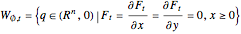 ,
, 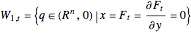 .
.
Typical multi-bifurcations of wavefronts in 2D and 3D are defined by generic reticular Legendrian unfoldings for the cases 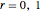 . Their generating families are stably reticular
. Their generating families are stably reticular  ‐
‐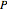 ‐
‐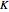 equivalent to one of the following:
equivalent to one of the following:
In the case 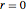 ,
,  :
:
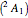
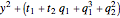 ,
,  ,
,
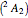
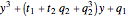 ,
, 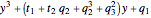 ,
,
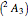
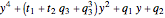 ,
,
In the case  :
:
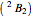
 ,
, 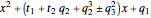 ,
,
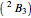
 ,
,
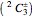
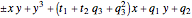 .
.
References
[1] V. I. Arnold, Singularities of Caustics and Wave Fronts, Dordrecht: Kluwer Academic Publishers, 1990.
[2] V. I. Arnold, S. M. Gusein–Zade, and A. N. Varchenko, Singularities of Differential Maps, Volume I: The Classification of Critical Points, Caustics and Wave Fronts (Monographs in Mathematics, Vol. 82), Basel: Birkhäuser, 1985.
[3] T. Tsukada, "Genericity of Caustics and Wavefronts on an  -Corner," Asian Journal of Mathematics, 14(3), 2010 pp. 335–358. projecteuclid.org/euclid.ajm/1295040754.
-Corner," Asian Journal of Mathematics, 14(3), 2010 pp. 335–358. projecteuclid.org/euclid.ajm/1295040754.
[4] T. Tsukada, "Bifurcations of Wavefronts on  -Corners: Semi-Local Classification," Methods and Applications of Analysis, 18(3), 2011 pp. 303–334. doi:10.4310/MAA.2011.v18.n3.a3.
-Corners: Semi-Local Classification," Methods and Applications of Analysis, 18(3), 2011 pp. 303–334. doi:10.4310/MAA.2011.v18.n3.a3.
[5] T. Tsukada. "Multi-Bifurcations of Wavefronts on  -Corners." arxiv.org/abs/1308.2274.
-Corners." arxiv.org/abs/1308.2274.
Permanent Citation