Multirate Signal Processing: Upsampling

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
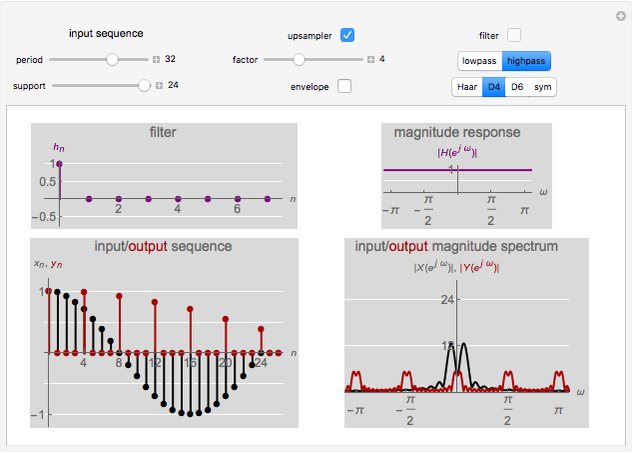
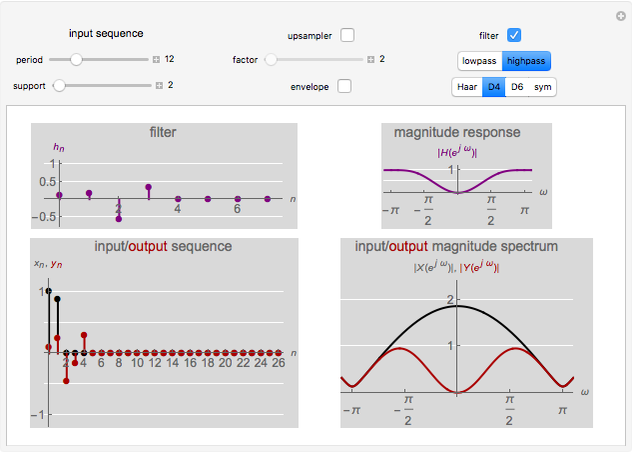
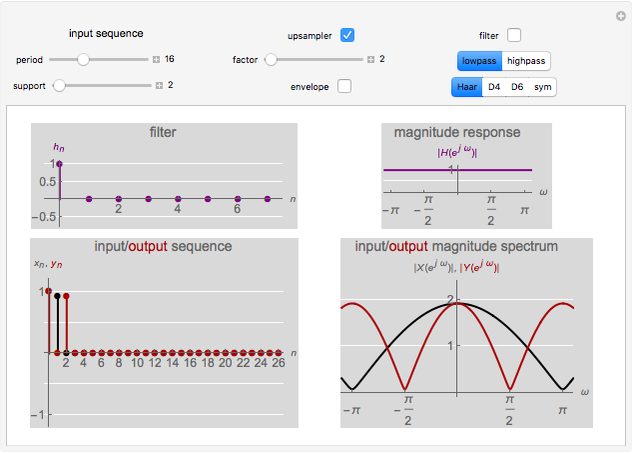
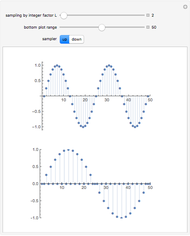
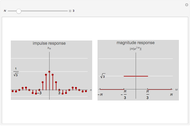
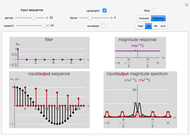
This Demonstration shows the effect of upsampling followed by filtering on a discrete-time sequence and its discrete-time Fourier transform (DTFT) spectrum. Upsampling by a factor of  inserts
inserts  zeros between every two samples of a discrete-time sequence. This expansion in time causes a contraction in frequency and the appearance of spurious spectral components, necessitating filtering after upsampling.
zeros between every two samples of a discrete-time sequence. This expansion in time causes a contraction in frequency and the appearance of spurious spectral components, necessitating filtering after upsampling.
Contributed by: Jelena Kovacevic (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Multirate signal processing is at the heart of most modern compression systems and standards, including JPEG, MPEG, and so on. Multirate refers to the fact that different sequences may have different time scales. One of the basic operations in multirate signal processing is upsampling.
Given a sequence  , its upsampled-by-
, its upsampled-by- version is
version is

Upsampling is only periodically shift invariant, since shifting the sequence by  will not necessarily lead to the upsampled output being shifted by
will not necessarily lead to the upsampled output being shifted by  .
.
If  is the DTFT spectrum of
is the DTFT spectrum of  , then
, then

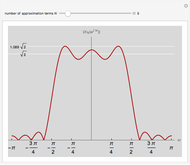
is the DTFT spectrum of  . The contracted versions of
. The contracted versions of  present in the output spectrum are called images. The contraction of frequencies can create frequency content not present in the original spectrum. Filtering after upsampling ensures that only the original spectrum is preserved after upsampling.
present in the output spectrum are called images. The contraction of frequencies can create frequency content not present in the original spectrum. Filtering after upsampling ensures that only the original spectrum is preserved after upsampling.
References
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Foundations of Signal Processing, Cambridge: Cambridge University Press, 2014. www.fourierandwavelets.org.
[2] M. Vetterli and J. Kovačević, Wavelets and Subband Coding, Englewood Cliffs, NJ: Prentice Hall, 1995. www.waveletsandsubbandcoding.org.
Permanent Citation