Gibbs Phenomenon in the Truncated Discrete-Time Fourier Transform of the Sinc Sequence
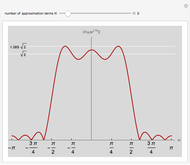
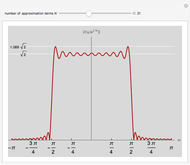
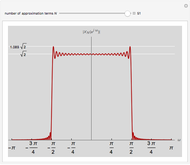
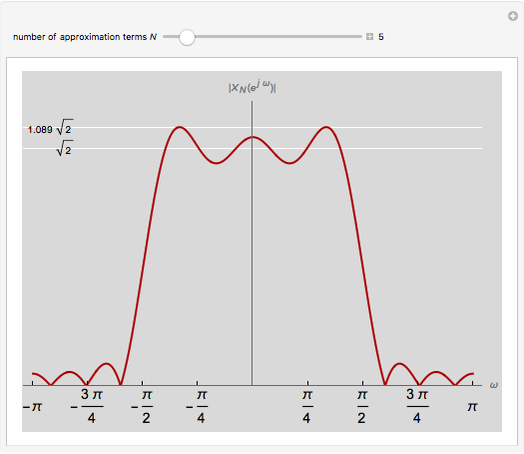
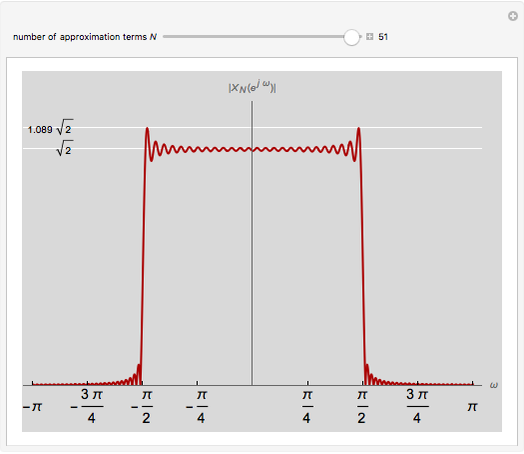
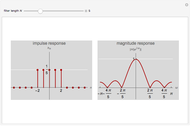
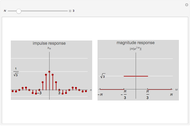
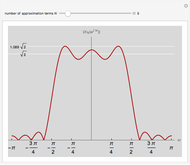
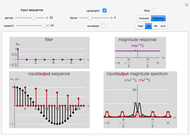
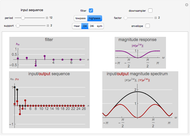
Using a finite number of terms of the Fourier series approximating a function gives an overshoot at a discontinuity in the function. This is called the Gibbs phenomenon. This Demonstration shows the same phenomenon with the discrete-time Fourier transform (DTFT) of a sinc sequence. The oscillations around the discontinuity persist with an amplitude of roughly 9% of the original height.
The Gibbs phenomenon was first observed in the 19th century, when trying to synthesize a square wave with a finite number of Fourier series coefficients. The oscillations around the discontinuities, while they became narrower, remained of constant amplitude even when more terms were added. This behavior was first attributed to flaws in the computation that was synthesizing the square wave, but J. Willard Gibbs in 1899 demonstrated that it was an actual mathematical phenomenon.
Reference
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Signal Processing: Foundations, Cambridge: Cambridge University Press, forthcoming. www.fourierandwavelets.org.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
