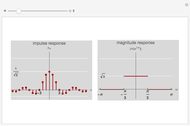
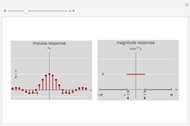
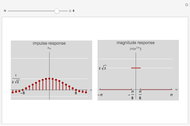
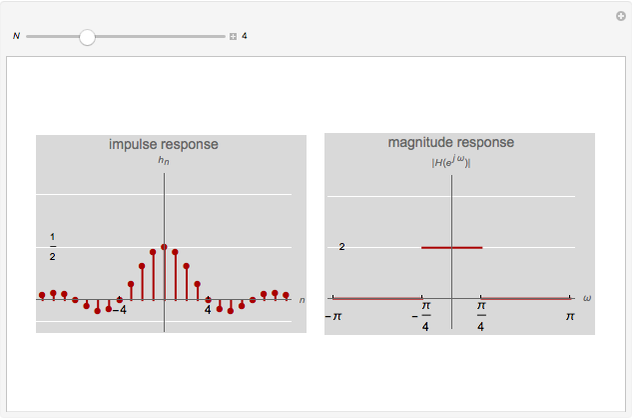
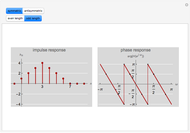
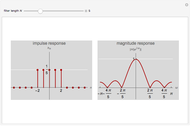
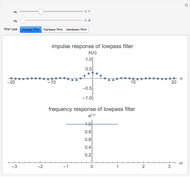
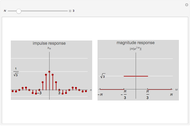
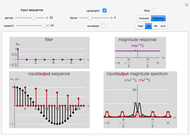
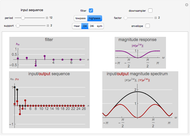
This Demonstration shows impulse and magnitude responses of ideal 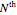-band low-pass discrete filters for 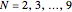. While such filters are not realizeable in practice, they serve as a desired template for passing certain frequencies while blocking others. The impulse response of an ideal low-pass filter is a sinc sequence (of unit norm in the figure), while its magnitude response is constant in the passband.
An ideal 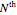-band discrete filter is a non-realizable filter whose magnitude response takes a single nonzero value in its passband. For example, an ideal low-pass filter passes frequencies below some cut-off frequency 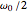and blocks the others; its passband is thus the interval .
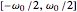The impulse response of an ideal low-pass 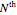-band filter is a sinc sequence; its unit-norm version is
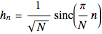for .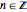
The impulse response at is thus (see figure).
The magnitude response of a unit-norm 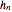is (see figure)
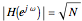for 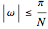, and 0 otherwise.
Reference
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Signal Processing: Foundations, Cambridge: Cambridge University Press, forthcoming. www.fourierandwavelets.org.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
