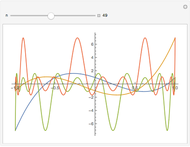
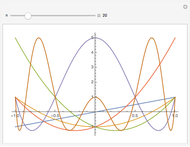
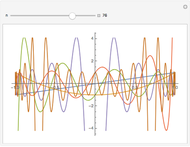
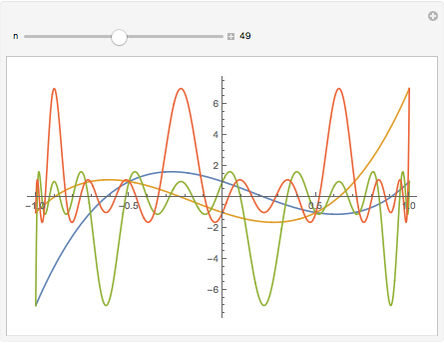
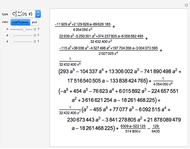
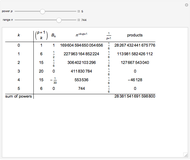
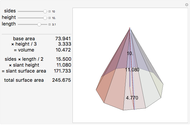
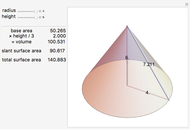
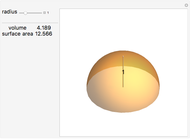
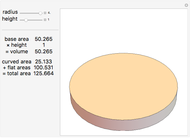
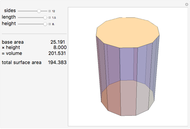
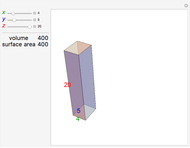
5-gon:  7-gon:
7-gon:  =
=  17-gon:
17-gon: 
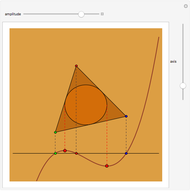
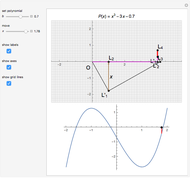
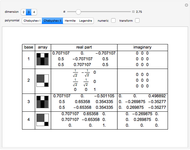
The 5-gon polynomial has roots  ,
, ,
, ,
,  }, where
}, where  is the golden ratio. Any one of these values can be used to construct a regular pentagon. The construction of a regular 17-gon (or heptadecagon) requires any root of the 17-gon polynomial. Gauss, as a teenager, showed that nested square roots can solve the 17-gon polynomial, making the 17-gon classically constructible. He also proved that roots of the 7-gon polynomial are not classically constructible. Curiously, any cubic equation can be solved with origami, making the heptagon origamically constructible.
is the golden ratio. Any one of these values can be used to construct a regular pentagon. The construction of a regular 17-gon (or heptadecagon) requires any root of the 17-gon polynomial. Gauss, as a teenager, showed that nested square roots can solve the 17-gon polynomial, making the 17-gon classically constructible. He also proved that roots of the 7-gon polynomial are not classically constructible. Curiously, any cubic equation can be solved with origami, making the heptagon origamically constructible.
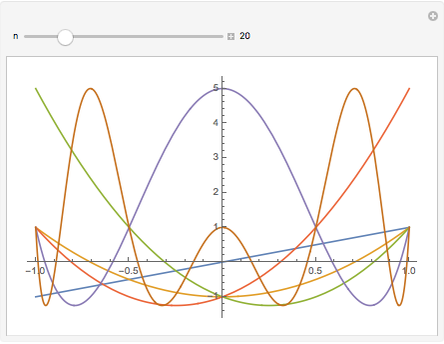
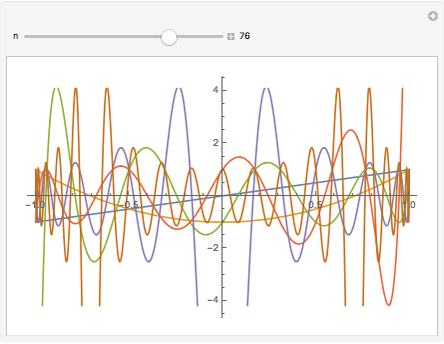
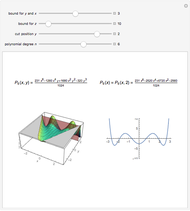
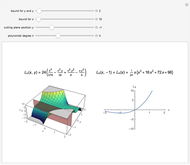
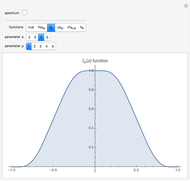
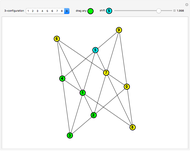
The  -gon polynomial is
-gon polynomial is  , a Chebyshev polynomial of the second kind. The graphs shown are of the factors of this Chebyshev polynomial.
, a Chebyshev polynomial of the second kind. The graphs shown are of the factors of this Chebyshev polynomial.
[less]