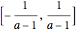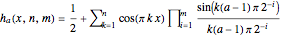Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Polynomial Atomic Functions for Fourier Analysis

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

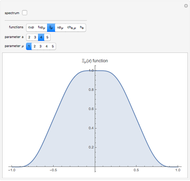
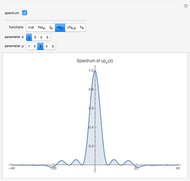
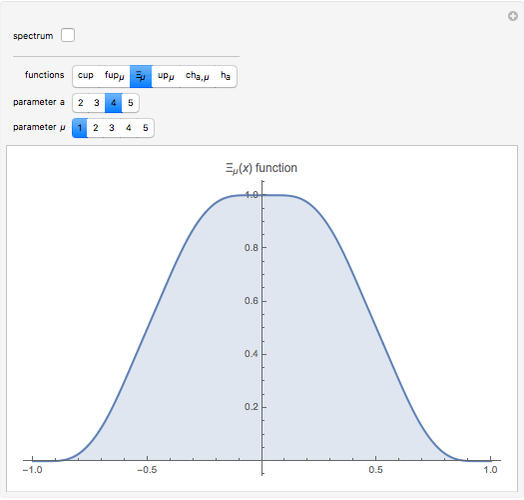
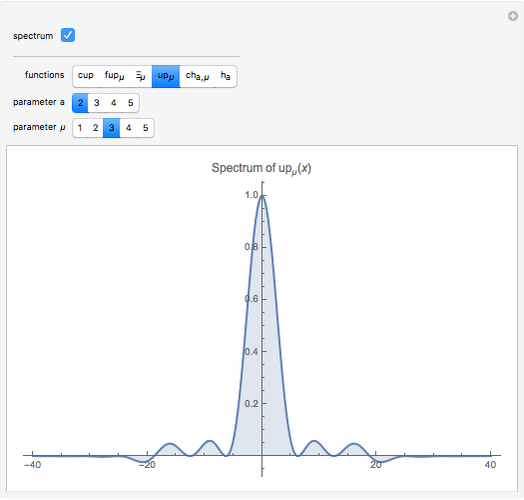
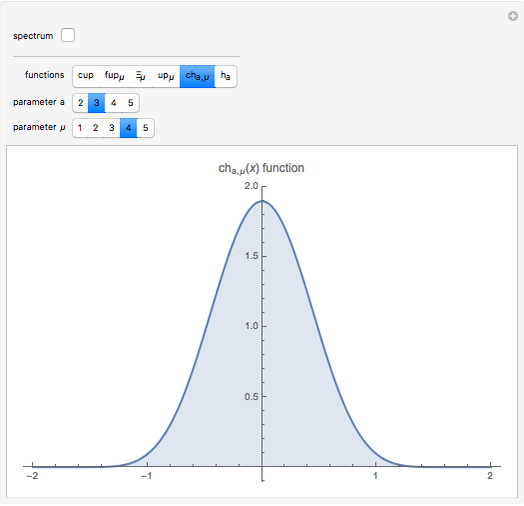
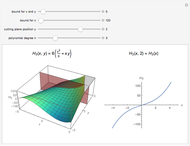
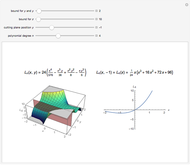
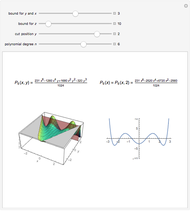
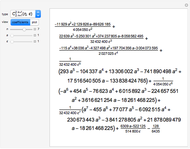
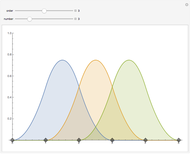
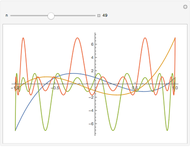
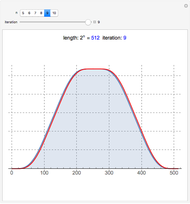
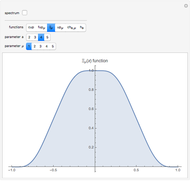
In computer terminology, an atomic process refers to a sequence of operations that can be executed by the CPU with a single instruction. (It has nothing to do with chemical atoms.) This Demonstration shows Fourier approximations (FA) of the family of polynomial atomic functions (pAF) and their Fourier transforms (spectrum). We consider a set of pAF, such as the functions 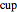, , 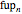, , 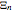, 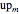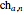and , each of which is defined as a finite solution of a coordinate functional differential equation (FDE) [1, 2].

[more]

For example, the function is a solution of the FDE of advanced type, , where and the support of is . The FA of is .

Here we use a FA technique to compute all the pAFs considered.

[less]

Contributed by: Oleg Kravchenko (December 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] V. F. Kravchenko, H. Perez-Meana, and V. I. Ponomaryov, Adaptive Digital Processing of Multidimensional Signals with Applications, Moscow: Fizmatlit, 2009.

[2] Y. Y. Konovalov, "Iterative Algorithms for Computation Convolutions of Atomic Functions Including New Family 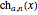," Proceedings of Days on Diffraction (DD) Conference, 2012, pp. 129–133. doi:10.1109/DD.2012.6402765.

[3] Y. Y. Konovalov and V. F. Kravchenko, "Weight Functions Based on the Convolutions of Atomic Functions," Proceedings of Days on Diffraction (DD) Conference, 2012, pp. 78–82. doi:10.1109/DD.2013.6712807.

[4] W. Hilberg, V. F. Kravchenko, O. V. Kravchenko, and Y. Y. Konovalov, "Atomic Functions and Generalized Thue–Morse Sequence in Digital Signal and Image Processing," Proceedings of MSMW International Kharkov Symposium, 2013, pp. 66–71. doi:10.1109/MSMW.2013.6621989.

[5] "Atomic Functions." (Nov 25, 2014) atomic-functions.ru/en.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send