Normal Approximation to a Binomial Random Variable

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
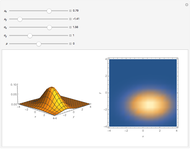
A binomial random variable with parameters  and
and  can be thought of as a sum of independent Bernoulli random variables, each with parameter
can be thought of as a sum of independent Bernoulli random variables, each with parameter  . The central limit theorem implies that for large values of
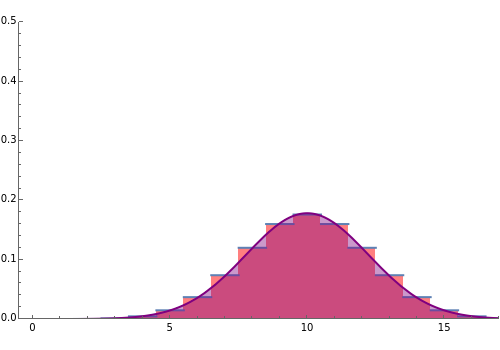
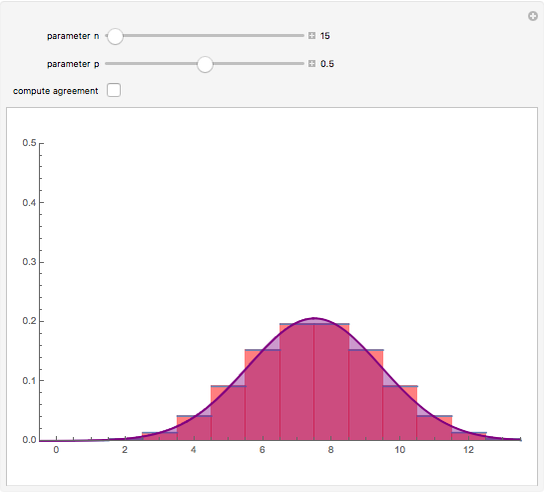
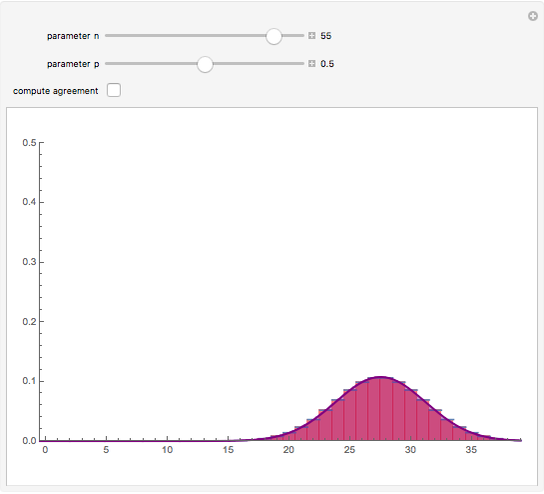
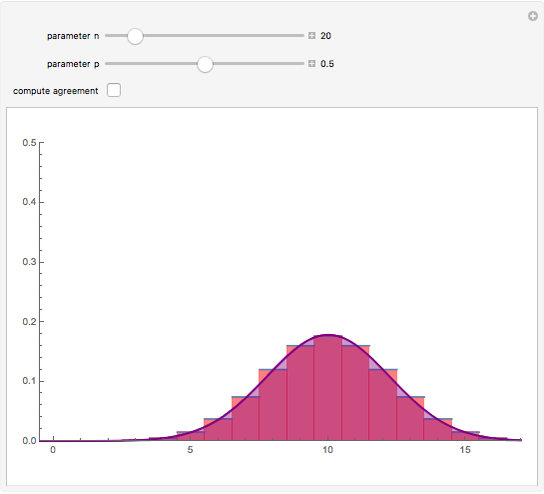
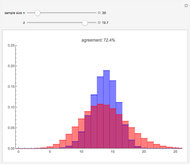
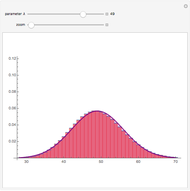
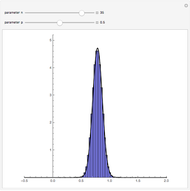
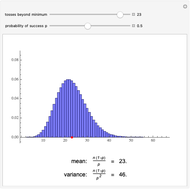
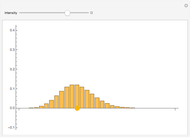
. The central limit theorem implies that for large values of  a binomial random variable can be well approximated by a normal random variable with the same mean and variance. A measure of agreement between the two is obtained by computing the purple area; 100% represents complete agreement between the two distributions. The computation of the purple area is slow, so use the sliders with the "compute agreement" box unchecked.
a binomial random variable can be well approximated by a normal random variable with the same mean and variance. A measure of agreement between the two is obtained by computing the purple area; 100% represents complete agreement between the two distributions. The computation of the purple area is slow, so use the sliders with the "compute agreement" box unchecked.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
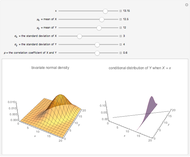
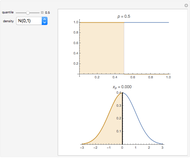
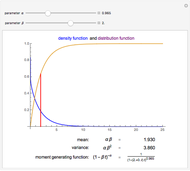
Snapshots
Details
detailSectionParagraphPermanent Citation
"Normal Approximation to a Binomial Random Variable"
http://demonstrations.wolfram.com/NormalApproximationToABinomialRandomVariable/
Wolfram Demonstrations Project
Published: March 7 2011