Random Values from Distributions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
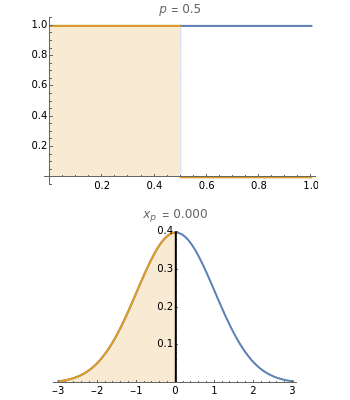
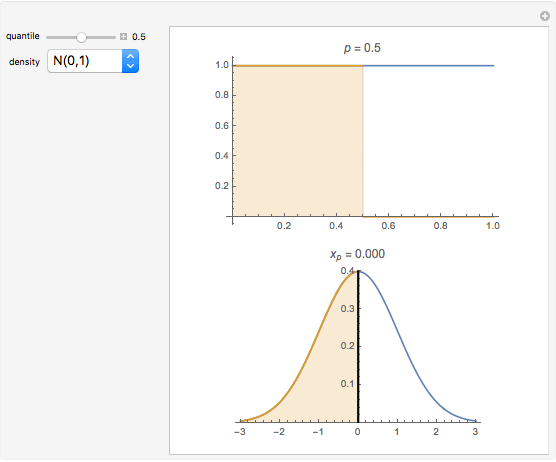
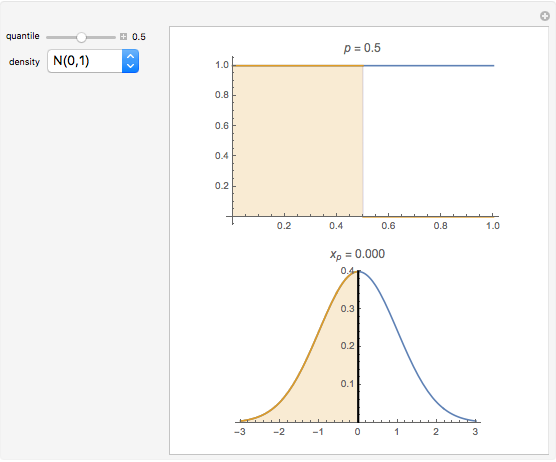
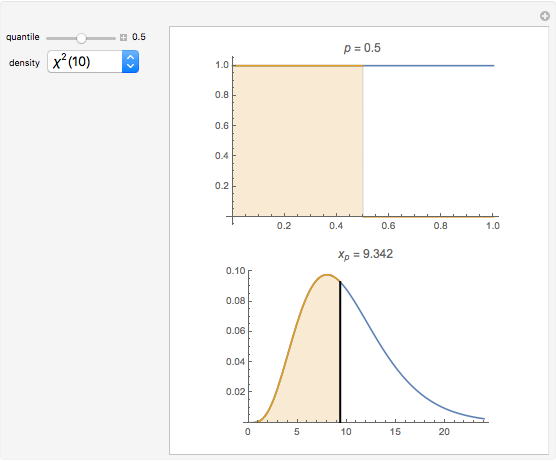
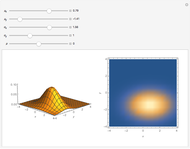
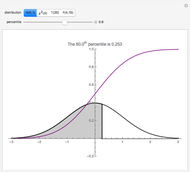
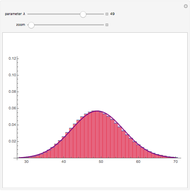
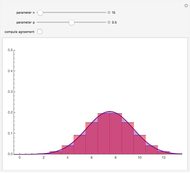
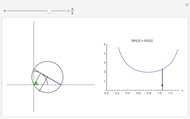
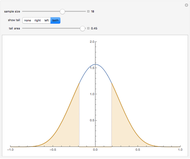
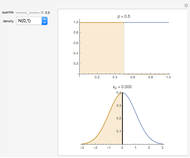
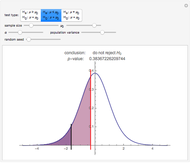
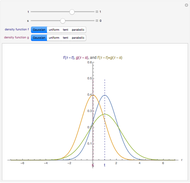
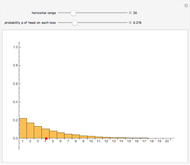
To observe values of a random variable that follows some arbitrary distribution, it is only necessary to be able to generate random numbers distributed uniformly in the unit interval and to compute quantiles of the desired distribution. (See the Demonstration "Using Rule 30 to Generate Pseudorandom Real Numbers" for a way to do the former.) The random number from the unit interval is simply used as the desired quantile of the more general distribution. That is, if  is the density function for the distribution from which a random value is to be drawn and
is the density function for the distribution from which a random value is to be drawn and  is a random number from the unit interval, the number
is a random number from the unit interval, the number  is taken such that the area to the left of
is taken such that the area to the left of  under
under  is equal to
is equal to  . Thus, the pink area is equal to
. Thus, the pink area is equal to  and the vertical line in the lower plot is at
and the vertical line in the lower plot is at  .
.
Contributed by: Chris Boucher (January 2008)
Open content licensed under CC BY-NC-SA
Details
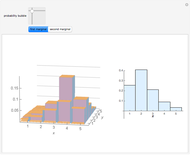
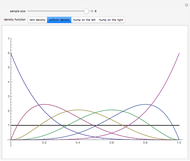
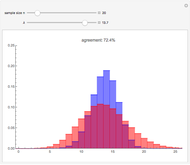
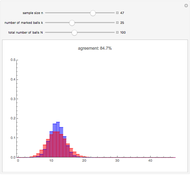
This Demonstration shows a general theoretical approach to generating random values from non-uniform distributions. Implementing it, however, requires computing the inverse of the cumulative distribution function (CDF) at the quantile in question. This can be computationally intensive if the CDF is complicated. In practice, random number generators often use other methods that are computationally faster.
Snapshots
Permanent Citation