Orthogonality as well as Equidistance Can Be Used as the Sole Primitive Notion for Euclidean Geometry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
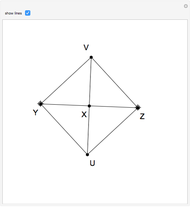
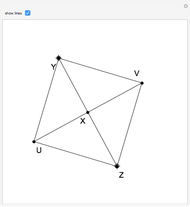
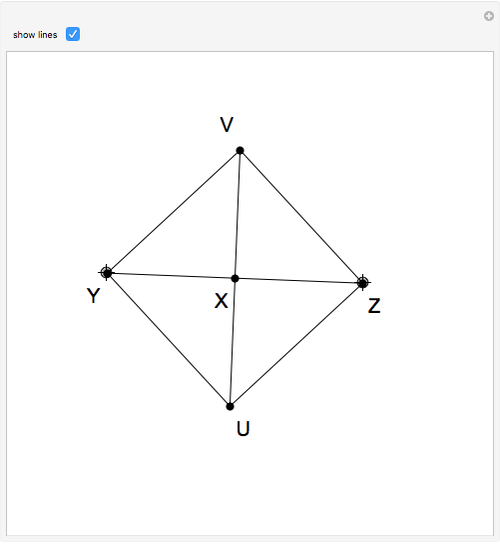
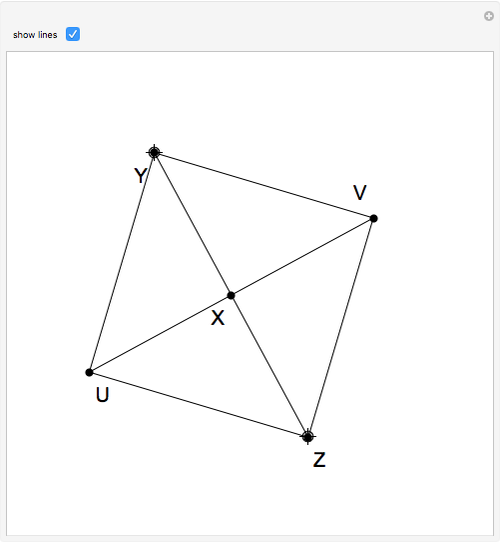
Pieri has shown that the ternary relation of a point  equally distant from two other points
equally distant from two other points  and
and  (in symbols,
(in symbols,  ) can be used as the primitive foundation of Euclidean geometry of two or more dimensions [1].
) can be used as the primitive foundation of Euclidean geometry of two or more dimensions [1].
Contributed by: Izidor Hafner (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
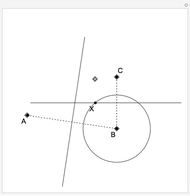
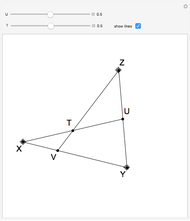
Definitions given in the caption are from [2].
Robinson's definitions of geometric relations using Pieri's relation [3, pp. 71–72] are:
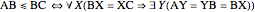




Here,  means
means  is between
is between  and
and  ;
;  means
means  ,
,  and
and  are collinear; and
are collinear; and  means
means  and
and  are symmetric about
are symmetric about  (i.e. that
(i.e. that  is the midpoint of
is the midpoint of  ).
).
References
[1] M. Pieri, "La Geometria Elementare istituita sulle nozioni di punto e sfera," Memorie di matematica e di fisica della Societ'a italiana delle Scienze, ser. 3(15), 1908 pp. 345–450.
[2] H. L. Royden, "Remarks on Primitive Notions for Elementary Euclidean and Non-Euclidean Plane Geometry," in Studies in Logic and the Foundations of Mathematics, Vol. 27, Amsterdam: North-Holland Publishing Company, 1959 pp. 86–96.
[3] R. M. Robinson, "Binary Relations as Primitive Notions in Elementary Geometry: The Axiomatic Method with Special Reference to Geometry and Physics," in Proceedings of an International Symposium Held at the University of California, Berkeley, December 26, 1957–January 4, 1958, Amsterdam: North-Holland Publishing Company, 1959 pp. 68–85. doi:10.1017/S0022481200092690.
Permanent Citation