Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Parametric Density Estimation Using Polynomials and Fourier Series

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

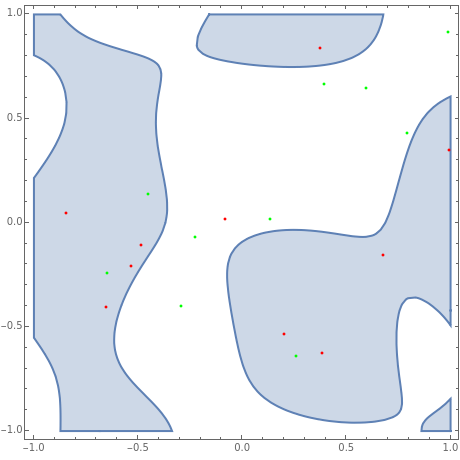
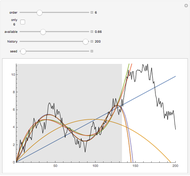
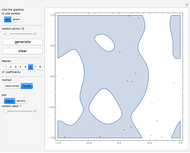
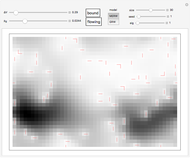
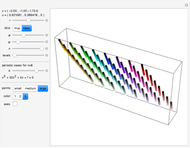
Imagine you obtain samples of two types, such as the red and green points in the graph shown here, and you would like to generalize by classifying some other points into one of these two classes. This is a basic problem in machine learning called supervised classification, with the class of each sampled point known. The standard approach is based on linear classifiers: using (hyper) planes for separation into two classes, analogous to its use in support vector machines or neural networks.

[more]

This Demonstration lets you play with direct nonlinear (two-class) classifiers in a 2D square: fitting a polynomial or Fourier series to the sample, using weights of opposite signs to distinguish the classes, followed by classification based on the sign of the difference of densities.

You can add points from the class of a chosen color by clicking its position. You can also generate some chosen number of random points. The "degree" controller lets you choose the degree of the polynomial. The number of coefficients used is shown below it. The "method" controller lets you switch between fitting a polynomial or a Fourier series. The "plot" controller lets you choose between RegionPlot and DensityPlot.

[less]

Contributed by: Jarek Duda (March 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

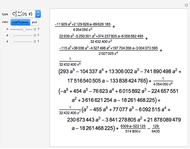
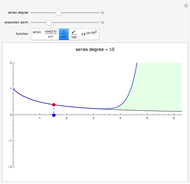
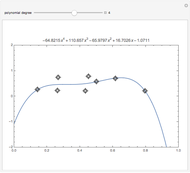
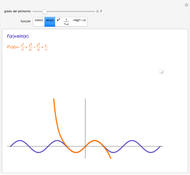
The method used for fitting density is described in [1]. The formula was derived by smoothing the sample through convolution with a kernel, then fitting a polynomial or Fourier series to the smoothed sample. It turns out that for mean-square fitting, we can perform the limit to a zero-width kernel, giving asymptotically optimal coefficients with a very simple formula.

Specifically, assuming orthonormal bases of functions (Legendre polynomials or sines and cosines here), the linear coefficient for a given function turns out to be just the average of the function over the sample:

,

where is the average of over the sample.

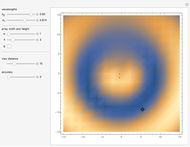
For the classification problem in this Demonstration, this density for green points was subtracted from the density for red points. Either the region of positive values (RegionPlot) or its density (DensityPlot) is then drawn.

Reference

[1] J. Duda, "Rapid Parametric Density Estimation." (Mar 14, 2017) arxiv.org/abs/1702.02144.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send