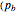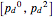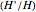Correction Trees

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Forward error correction methods are fundamental in the transmitting and storing of information. They allow increasing the size of the message using so-called redundancy to be able to repair errors of assumed statistics, for instance that each bit can be changed with probability 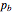 . In the standard approach we encode the message in independent blocks.
. In the standard approach we encode the message in independent blocks.
Contributed by: Jarek Duda (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This new correction mechanism (that when trying a wrong correction at each step, the probability of realising it is 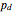 ), can be constructed using an entropy coder like an asymmetric numeral system. The correction mechanism can be implemented by inserting an additional forbidden symbol with probability
), can be constructed using an entropy coder like an asymmetric numeral system. The correction mechanism can be implemented by inserting an additional forbidden symbol with probability 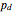 and rescaling the probabilities of the original symbols. Now after an error the decoder will produce a random symbol sequence—at each step the decoder has
and rescaling the probabilities of the original symbols. Now after an error the decoder will produce a random symbol sequence—at each step the decoder has 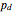 probability of spotting that something was wrong. This approach does not work for all block lengths—for very large noise, methods from fig. 3 of the paper below can be used.
probability of spotting that something was wrong. This approach does not work for all block lengths—for very large noise, methods from fig. 3 of the paper below can be used.
If before adding redundancy, each step was encoded with an average  bits, adding this forbidden symbol makes the average
bits, adding this forbidden symbol makes the average 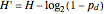 bits: the size of the message grows by
bits: the size of the message grows by 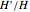 times.
times.
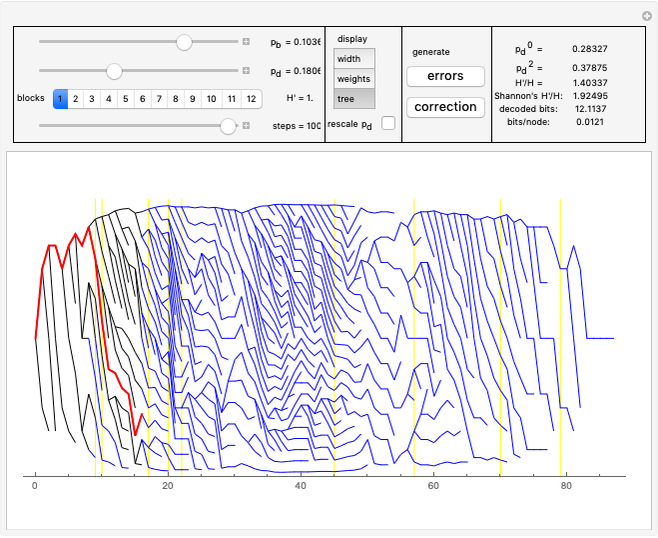
To expand the tree, we have to choose the most probable node. To do this we calculate for each node some weight and at each step we choose the leaf with the largest weight.
The weight of the given correction (using Bayesian analysis) is 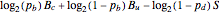 , where
, where 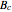 is the number of changed bits,
is the number of changed bits, 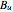 is the number of unchanged bits, and
is the number of unchanged bits, and 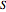 is the number of steps. That means the longer the correction and the less bits it changes, the better.
is the number of steps. That means the longer the correction and the less bits it changes, the better.
We assume symmetric memoryless statistics of errors. That means each bit has 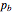 probability of being changed. The control slider for this parameter is logarithmic.
probability of being changed. The control slider for this parameter is logarithmic.
The value 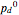 corresponds to the theoretical (Shannon's) limit. Below this limit it is impossible to correct, given the statistics of errors. In the approach presented here, below this value the weight of the proper correction no longer grows statistically and so the tree would immediately grow exponentially. The approach presented here should work well asymptotically above
corresponds to the theoretical (Shannon's) limit. Below this limit it is impossible to correct, given the statistics of errors. In the approach presented here, below this value the weight of the proper correction no longer grows statistically and so the tree would immediately grow exponentially. The approach presented here should work well asymptotically above 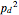 . In the range
. In the range 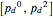 the tree has generally small width, but rare large error concentrations implies that the expected width will be asymptotically infinite.
the tree has generally small width, but rare large error concentrations implies that the expected width will be asymptotically infinite.
In one step we process one block of bits—their lengths are generally chosen randomly from some set. Each split of the tree corresponds to some correction of the currently processed block. We assume that the block lengths are chosen equally probable. The average number of bits processed in one step 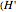 ) is the average length of a block.
) is the average length of a block.
To be able to compare different parameters, the distribution of errors is changed only if 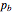 is changed or the "errors" button is pressed.
is changed or the "errors" button is pressed.
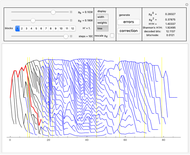
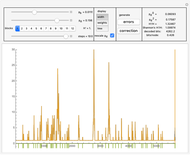
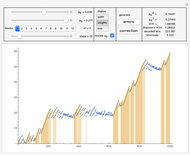
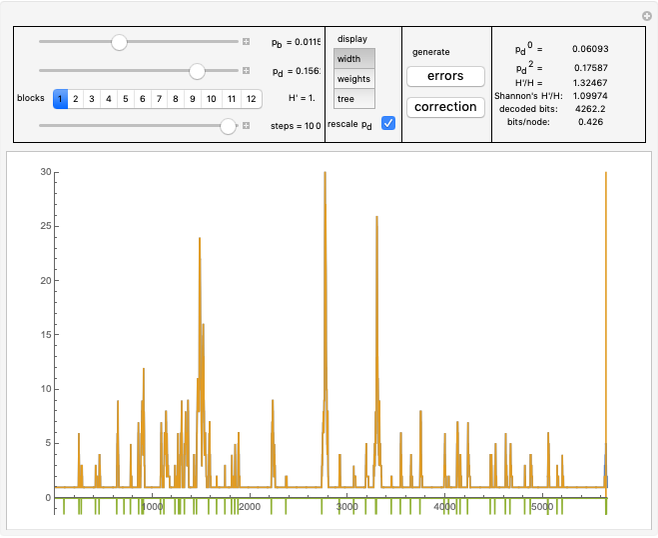
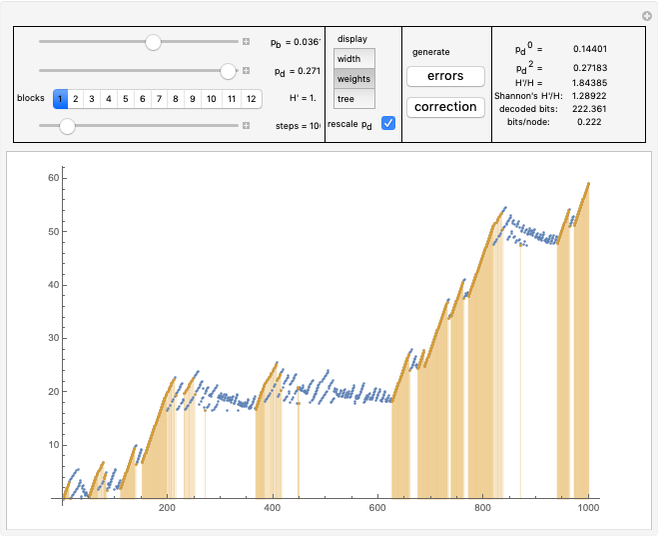
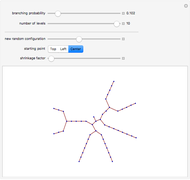
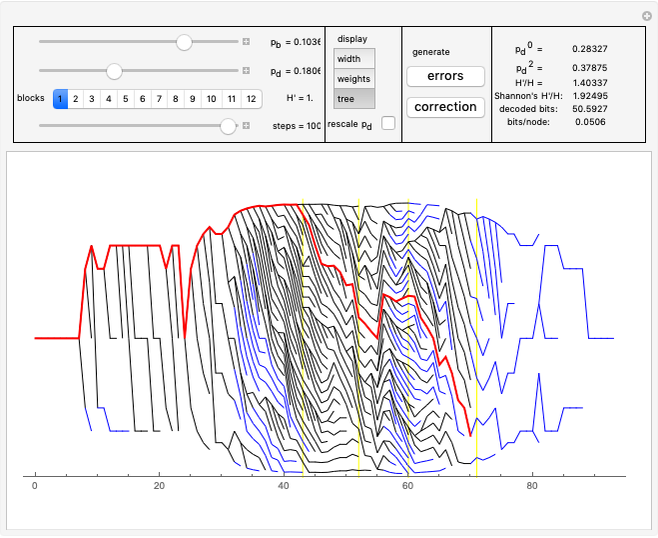
In "widths" mode, the positions of the errors are marked with yellow spikes. There are two lines: the blue line shows the width of the whole tree. The red vertical line shows the last position of proper correction. This red line shows the width assuming that it was the end of the correction. The difference between these lines represents subtrees of wrong corrections created while trying to correct the last error. We see that literally redundancy is transferred to help with local error concentrations.
In "weight" mode we see the best weights chosen in succeeding steps. The red dots with filling are proper corrections and the blue ones correspond to steps of wrong correction. We see that the weight generally grows, but locally can dramatically drop what require a very large number of steps/nodes to repair.
In "tree" mode yellow lines represent errors and the red path is the proper correction. Proceeding step by step we can see how the algorithm tries to find the proper branch.
More details can be found in the  section of Asymmetric numeral systems.
section of Asymmetric numeral systems.
Permanent Citation