Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Hypocycloids

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

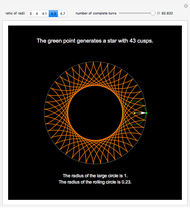
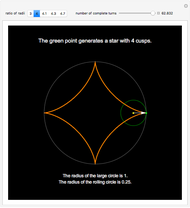
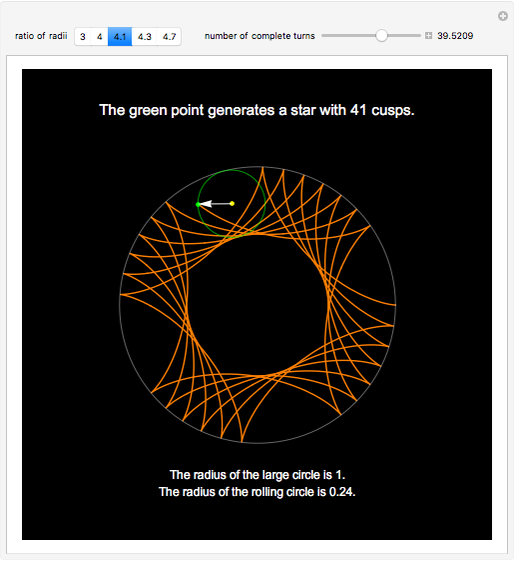
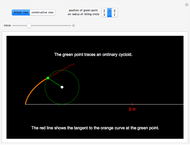
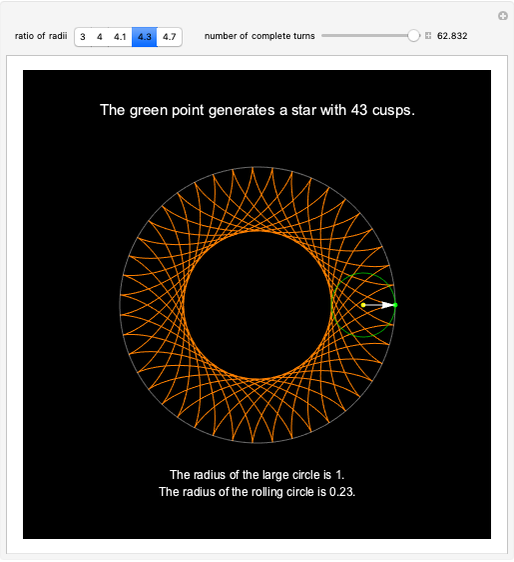
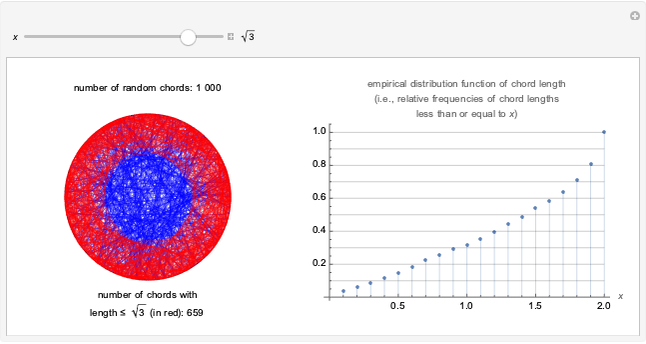
A hypocycloid is the path of a point fixed to the green circle rolling inside the white circle. If the ratio of the two radii is an integer, we get an ordinary star. If the ratio is rational and not an integer, we get a self-intersecting star. If the ratio is irrational, the curve does not close.

Contributed by: Tomas Garza (December 2019)
Open content licensed under CC BY-NC-SA

Details

A hypocycloid [1] is the curve generated by tracing the path of a fixed point on a circle that rolls inside a larger circle. When the ratio of the radius of the larger cycle to that of the smaller one is an integer (), the curve obtained is an -cusp star. Otherwise, the curve obtained is a multi-spiked star, with spikes.

This Demonstration gives a few examples of this amusing behavior. Move the slider to observe the development of the curve as the inside circle rolls on.

Reference

[1] Wikipedia. "Hypocycloid." (Dec 10, 2019) en.wikipedia.org/wiki/Hypocycloid.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send