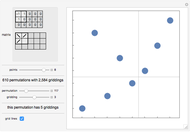
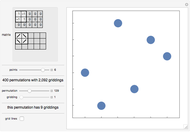
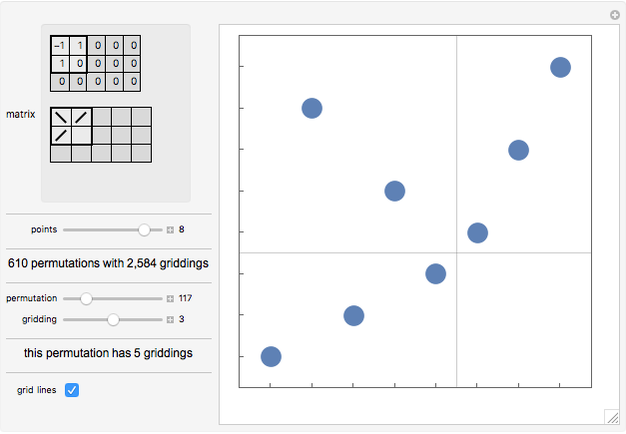
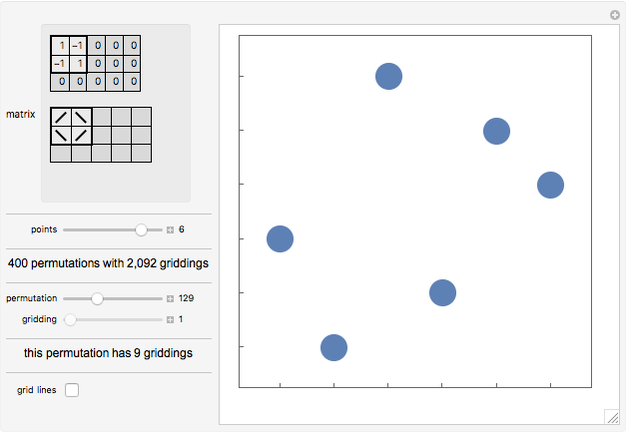
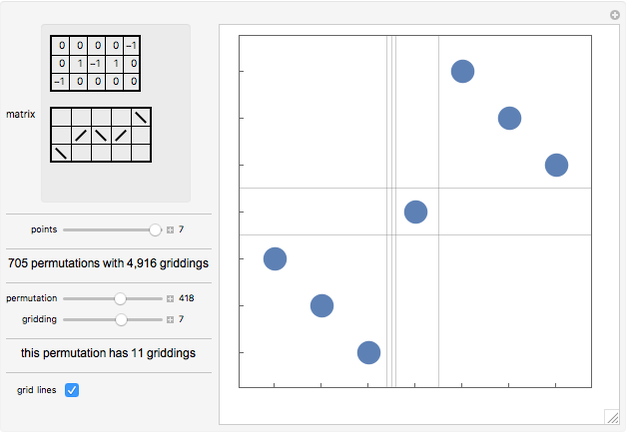
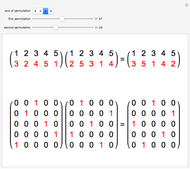
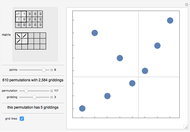
A grid class of permutations is defined by a 0/1/-1 matrix, which specifies the shape of plots of the permutations in the class. Each cell in the matrix corresponds to a rectangle in a "gridding" of a permutation. If the cell in the matrix contains 1, any points in the rectangle must form an increasing sequence; if the cell contains -1, any points in the rectangle must form a decreasing sequence; if the cell is 0, the rectangle must be empty. An empty sequence is both increasing and decreasing. A permutation in a grid class may have multiple possible griddings.