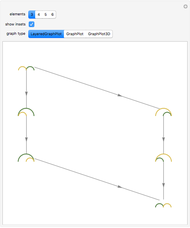
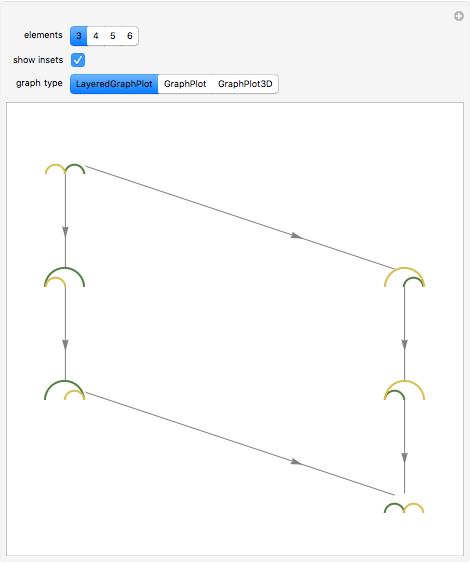
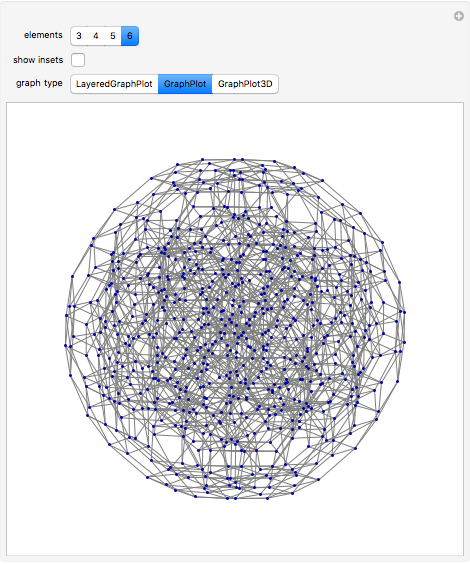
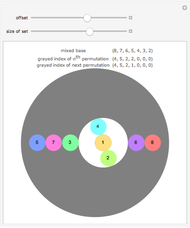
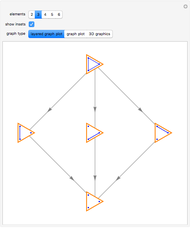
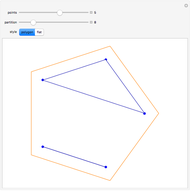
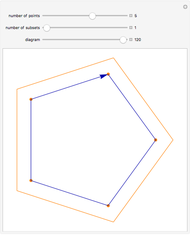
This Demonstration shows the lattice formed by sets of permutations ordered by inversions. Arrows in the lattice connect two permutations when one can be transformed to the other by inverting an adjacent pair of elements. The number of permutations at the level , , is the coefficient of in the expansion of , and the sum of those coefficients is .
Snapshot 1: considering the permutations of , for example, the number of permutations at each level corresponds to the coefficients of in the expansion of
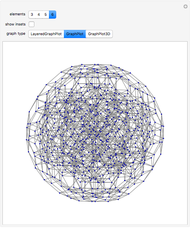
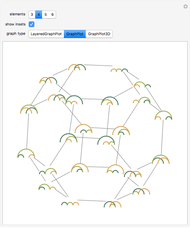
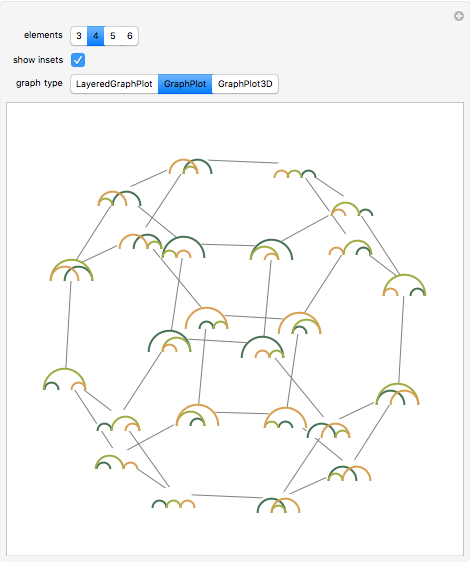
Snapshot 2: for graphs with large numbers of vertices, clearing the "show insets" option can better show the overall structure of the lattice
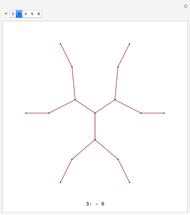
Snapshot 3: other visualizations are available by changing the "graph type" option
References
[1] R. P. Stanley, Enumerative Combinatorics, Vol. 1, Cambridge: Cambridge University Press, 1997.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
