Phonon Dispersion Relation in Brillouin Zone

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
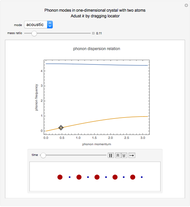
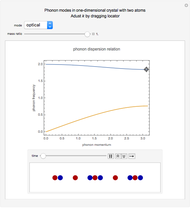
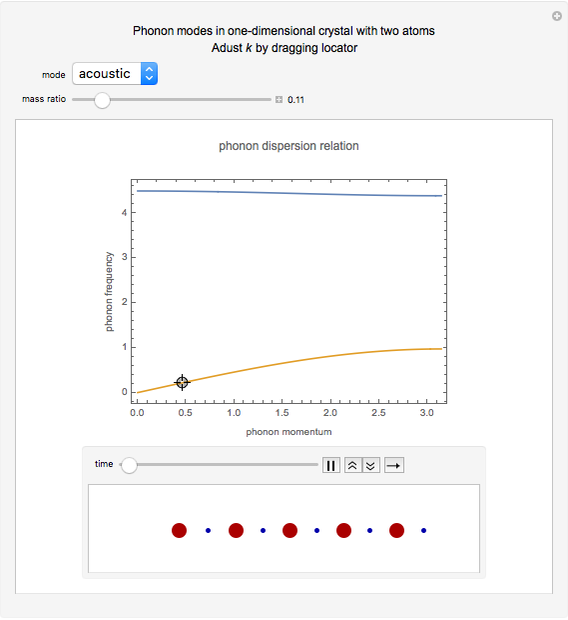
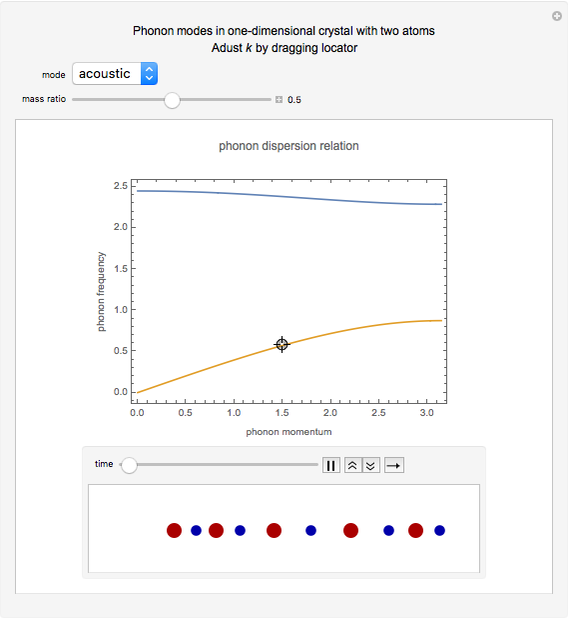
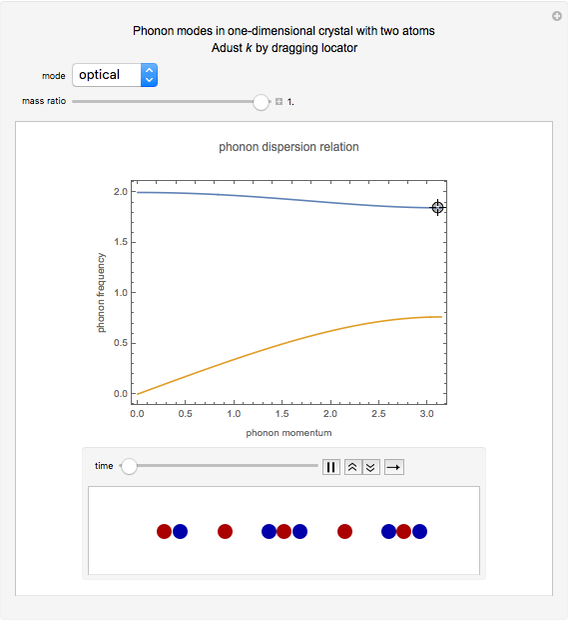
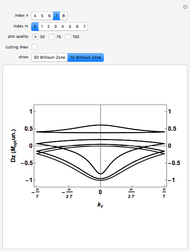
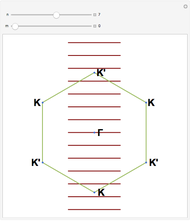
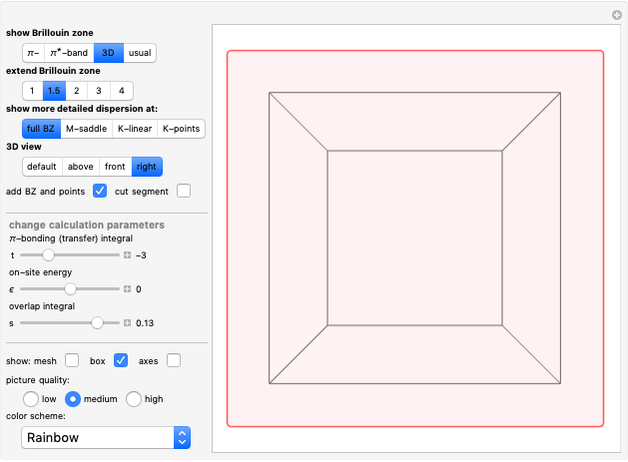
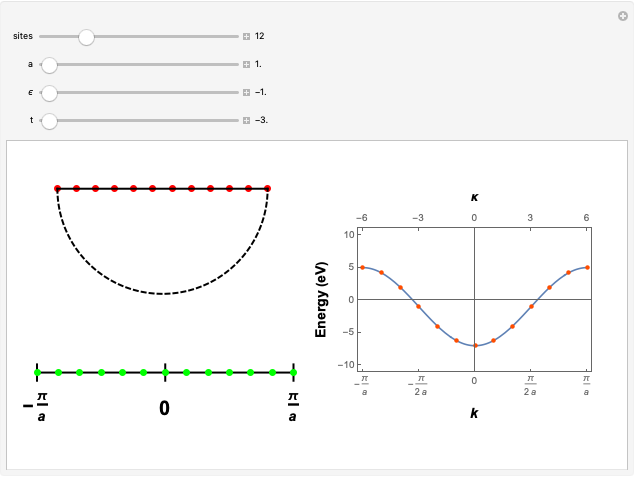
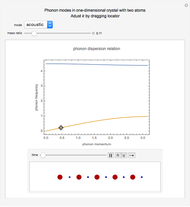
This Demonstration models the phonon dispersion relation within the Brillouin zone of a crystal. The top of the graphic shows the dispersion relation, while the bottom shows an animation of the collective vibration of the atoms in the crystal. You can observe the effects of both the acoustic and optical modes of phonons on the group velocity of the atoms in a crystal. Near the edge of the Brillouin zone, the group velocity approaches zero.
Contributed by: W. Craig Carter and Tara Sarathi (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A phonon is a collective vibration of atoms in a crystal. A dispersion relation gives the angular frequency of the phonon  as a function of the momentum of the phonon
as a function of the momentum of the phonon  . The slope of the corresponding plot gives the group velocity of vibration of the atoms, which is also the speed of sound in the crystal.
. The slope of the corresponding plot gives the group velocity of vibration of the atoms, which is also the speed of sound in the crystal.
Since a perfect crystal is a periodic structure, the behavior of the phonons within this crystal is only modeled within one Brillouin zone. Each Brillouin zone represents one unit cell in reciprocal space. If the Brillouin zone contains more than one atom, then two different modes of phonons occur: the acoustic mode and the optical mode. The acoustic mode corresponds to sound waves traveling through the crystal, while the optical mode can interact either directly or indirectly with light.
At the edge of this Brillouin zone, the group velocity of the phonon approaches zero, thus creating a standing wave.
Permanent Citation
"Phonon Dispersion Relation in Brillouin Zone"
http://demonstrations.wolfram.com/PhononDispersionRelationInBrillouinZone/
Wolfram Demonstrations Project
Published: April 13 2011