Pins, Fins and Staggered Fins on Heat-Transfer Panels

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
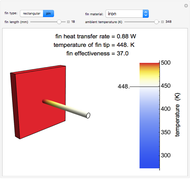
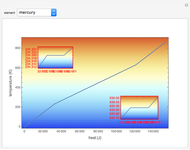
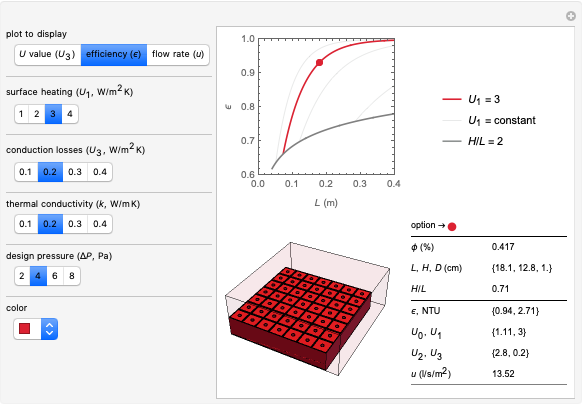
This Demonstration shows how to optimize the heat-transfer performance of a flat vertical panel by changing its surface geometry.
[more]
Contributed by: Remy Fortin and Salmaan Craig (November 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
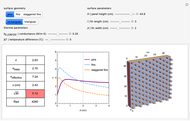
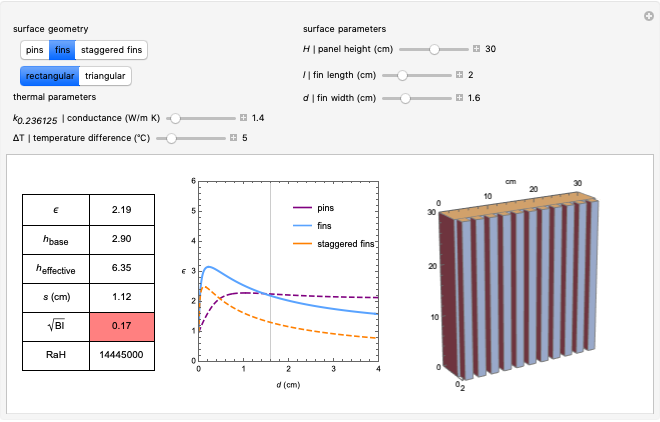
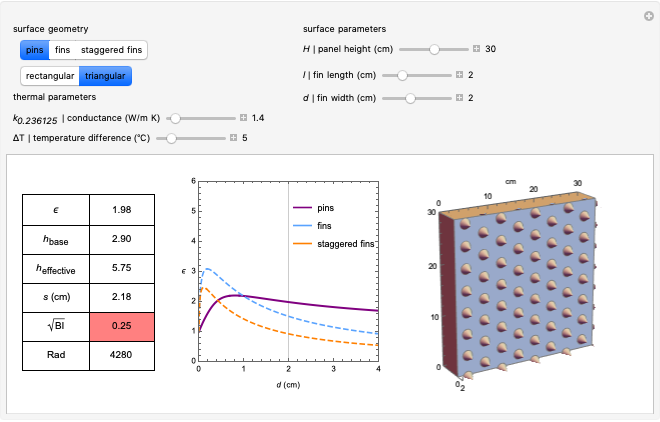
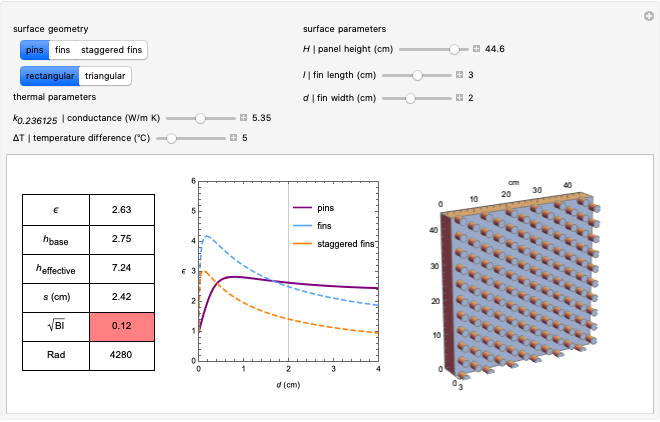
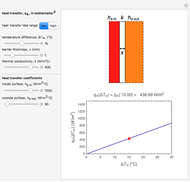
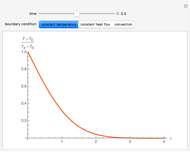
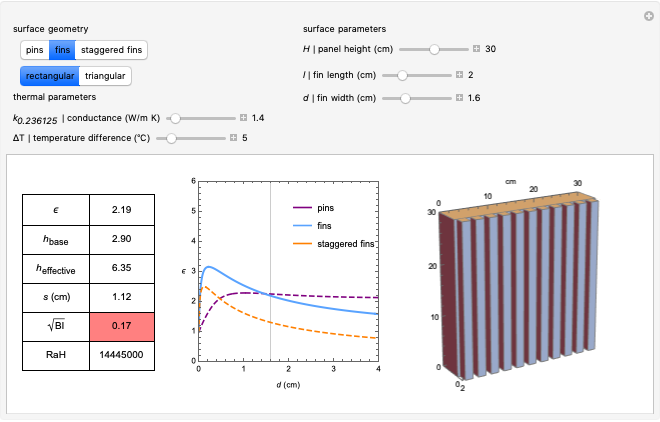
In 1993, Bejan described how to calculate the enhancement of heat transfer between a solid surface and a fluid when the thermal contact is increased through a change in the surface geometry [3]. With Lorente, he later described how to determine the optimal spacing between the features added to the solid surface [4]. This Demonstration combines these two contributions to calculate the effectiveness of these heat-transfer enhancements for a solid surface with optimally spaced features. The relevant parameters are listed below.
Thermal Parameters
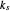 : Conductivity of the panel material in
: Conductivity of the panel material in 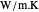 . Assume that the panel and the features share the same conductivity (same material).
. Assume that the panel and the features share the same conductivity (same material).
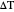 : Temperature difference between the panel and the air with which it is exchanging heat in Celsius.
: Temperature difference between the panel and the air with which it is exchanging heat in Celsius.
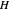 : Panel height in meters. The width of the panel has no impact on the effectiveness.
: Panel height in meters. The width of the panel has no impact on the effectiveness.
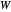 : Panel width in meters. The width of the panel has no impact on the effectiveness. By default, it is set equal to
: Panel width in meters. The width of the panel has no impact on the effectiveness. By default, it is set equal to 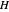 .
.
 : Fin width or pin diameter in meters.
: Fin width or pin diameter in meters.
 : Length of the features in meters from the surface of the panel to the tip.
: Length of the features in meters from the surface of the panel to the tip.
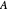 (for staggered fins): Dimensionless contact area.
(for staggered fins): Dimensionless contact area. 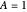 means perfectly staggered fins. The range of the slider is fixed between 0.4 and 1.2 to match the range of correlation from the papers.
means perfectly staggered fins. The range of the slider is fixed between 0.4 and 1.2 to match the range of correlation from the papers.
 (for staggered fins): The number of fin surfaces facing an elemental (vertical) channel.
(for staggered fins): The number of fin surfaces facing an elemental (vertical) channel.
Table of Results
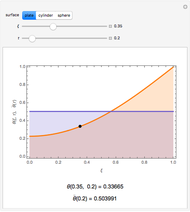
 : Effectiveness of the panel as a dimensionless ratio
: Effectiveness of the panel as a dimensionless ratio  [3]. The maximum effectiveness for each type of feature can be read off the graph. The table turns red when
[3]. The maximum effectiveness for each type of feature can be read off the graph. The table turns red when  is below 1, because at this point the panel with features becomes less effective than the panel without features.
is below 1, because at this point the panel with features becomes less effective than the panel without features.
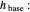 Heat-transfer coefficient of a base panel without features in
Heat-transfer coefficient of a base panel without features in 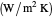 .
.
 Effective heat-transfer coefficient of the panel with features in
Effective heat-transfer coefficient of the panel with features in  .
.
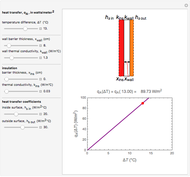
 : Optimal spacing in meters between features from edge to edge.
: Optimal spacing in meters between features from edge to edge.
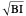 : This model is valid when
: This model is valid when 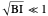 as per [3] equations 2.129 and 2.130. The table turns red when the square root of the Biot number is more then 0.1.
as per [3] equations 2.129 and 2.130. The table turns red when the square root of the Biot number is more then 0.1.
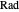 (for pins): Rayleigh number for the width of a single pin. The equations used "agree within 1.7% in the range
(for pins): Rayleigh number for the width of a single pin. The equations used "agree within 1.7% in the range 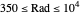 " [4] p. 89. The result table turns red when the Rayleigh number is outside that range.
" [4] p. 89. The result table turns red when the Rayleigh number is outside that range.
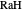 (for fins): Rayleigh number for the panel height.
(for fins): Rayleigh number for the panel height.
 (for staggered fins): Rayleigh number for the panel height. The equations used "are accurate within 6% in the range
(for staggered fins): Rayleigh number for the panel height. The equations used "are accurate within 6% in the range 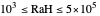 " [4] p. 88. The table turns red when the Rayleigh number is outside that range.
" [4] p. 88. The table turns red when the Rayleigh number is outside that range.
References
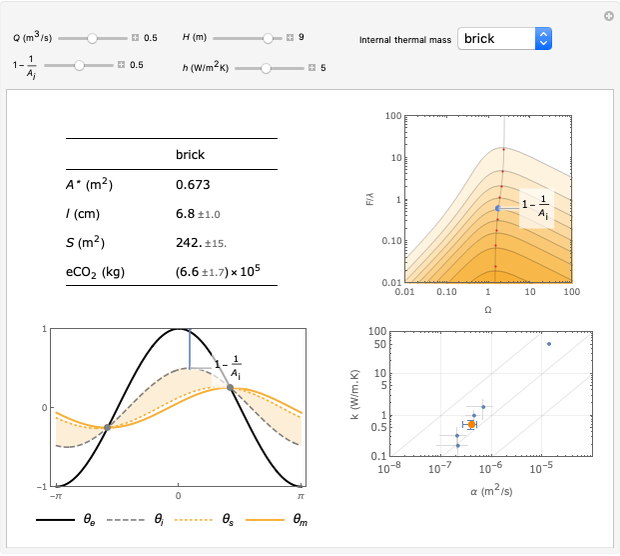
[1] S. Craig, "The Optimal Tuning, within Carbon Limits, of Thermal Mass in Naturally Ventilated Buildings," Building and Environment, 165, 2019. doi:10.1016/j.buildenv.2019.106373.
[2] S. Craig and R. Fortin, "How to Design a Building So It Works Like a Termite Mound," from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/HowToDesignABuildingSoItWorksLikeATermiteMound.
[3] A. Bejan, Heat Transfer, New York: John Wiley & Sons, Inc., 1993.
[4] A. Bejan and S. Lorente, Design with Constructal Theory, Hoboken, NJ: John Wiley & Sons, 2008.
[5] G. A. Ledezma and A. Bejan, "Optimal Geometric Arrangement of Staggered Vertical Plates in Natural Convection," Journal of Heat Transfer, 119(4), 1997 pp. 700–708. doi:10.1115/1.2824174.
[6] A. Bejan, A. J. Fowler and G. Stanescu, "The Optimal Spacing between Horizontal Cylinders in a Fixed Volume Cooled by Natural Convection," International Journal of Heat and Mass Transfer, 38(11), 1995 pp. 2047–2055. doi:10.1016/0017-9310(94)00312-J.
Permanent Citation