Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dynamics of Seasonal Epidemics

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

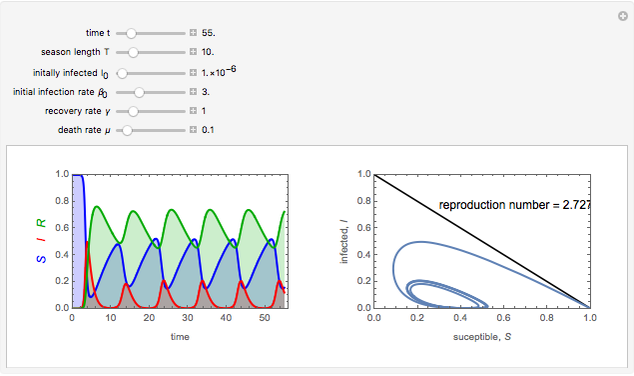
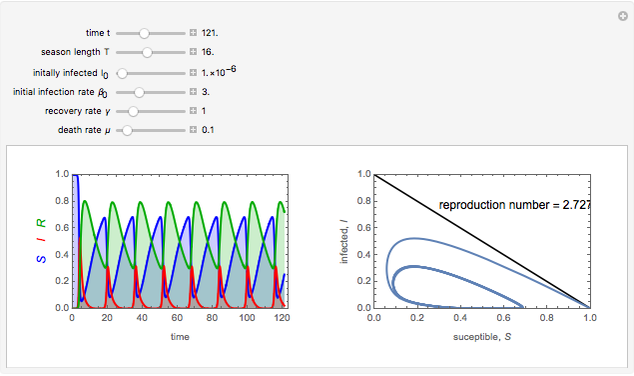
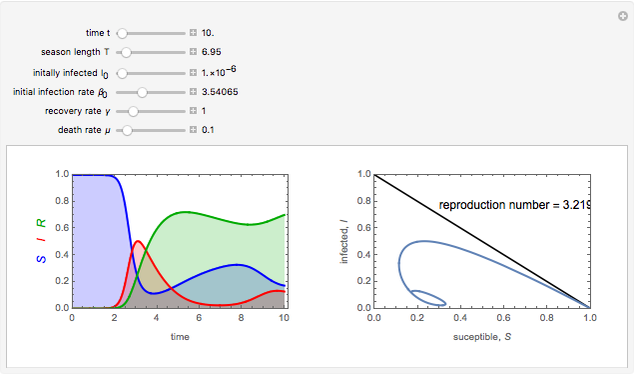
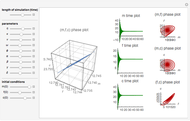
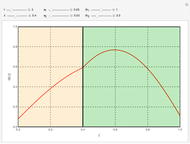
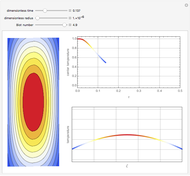
To study how the probability of getting a disease varies with the seasons of the year, this Demonstration analyzes a susceptibility-infection-recovery (SIR) model with a periodically varying infection rate. The model is a set of nonlinear differential equations with periodically varying parameters.

Contributed by: Clay Gruesbeck (November 2012)
Open content licensed under CC BY-NC-SA

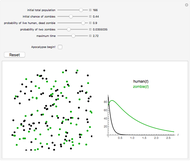
Snapshots

Details

The periodically forced SIR model is:

,

,

.

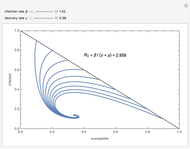
Here , , and are the fractions of susceptible, infective, and recovered individuals in the population; is the birth and death rate; is the seasonally dependent infection rate; and is the recovery rate. We take to be periodic; , where is the length of the infection season and is a constant. The reproduction number for this system is ; if the integral is greater than one, the disease will not disappear and may undergo interesting and complex phenomena of nonlinear parametric resonance [1].

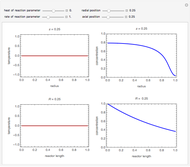
You can vary the time window of observation, the length of the infection season, the fraction initially infected, and the rates of initial infection, recovery, and death to follow the trajectory of the SIR system.

Reference

[1] Wikipedia. "Compartmental Models in Epidemiology." (Jul 2, 2012) en.wikipedia.org/wiki/Compartmental_models_in _epidemiology.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send