Probability Density for a Classical Harmonic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
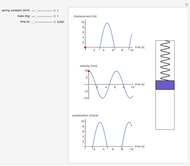
A classical harmonic oscillator with mass  and spring constant
and spring constant  has a total energy
has a total energy  , dependent on its amplitude
, dependent on its amplitude  . We determine the probability density
. We determine the probability density  as the position
as the position  varies between
varies between  and
and  , making use of its oscillation frequency
, making use of its oscillation frequency  (or period
(or period  ). Thus we find the probability density function
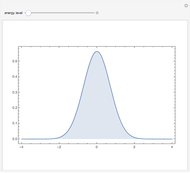
). Thus we find the probability density function  where representing the probability that the mass would be found in the infinitesial interval
where representing the probability that the mass would be found in the infinitesial interval  to
to  .
.
Contributed by: Muhamad Hamdi and Walana Yumna Aribah (January 2012)
Open content licensed under CC BY-NC-SA
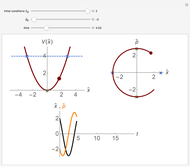
Snapshots
Details
Given a classical harmonic oscillator with particle mass  , much can be calculated using the principle of energy conservation. We have
, much can be calculated using the principle of energy conservation. We have
 ,
,
where  is the oscillating amplitude and
is the oscillating amplitude and  is the displacement. We need to find the result of integration for the period
is the displacement. We need to find the result of integration for the period  ,
,
 .
.
Therefore we obtain the probability density function as a function of its total energy and displacement
 ,
,
 .
.
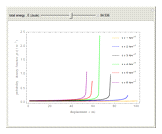
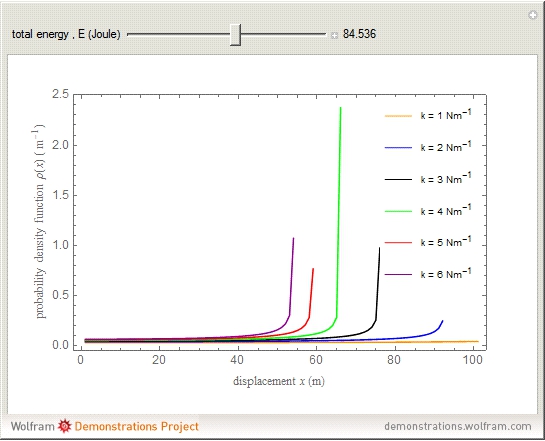
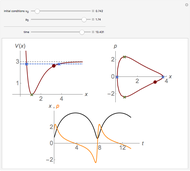
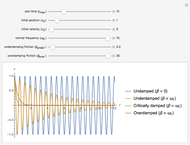
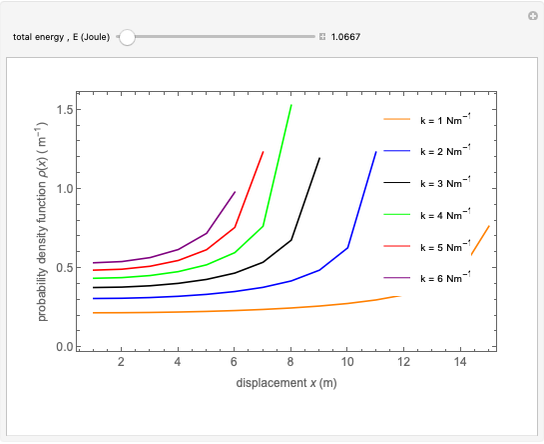
The result of classical harmonic oscillator mechanical behavior analyzed by the probability density function shows that the characteristic of this density function 
 with six kinds of spring constants, where
with six kinds of spring constants, where  varies from
varies from  to
to  .
.
Snapshots 1, 2, 3, and 4 describe the behavior of the density function for six different spring constants moving simultaneously from its equilibrium point with the given total energy. The density function is plotted against its change of particle position. Graphs show that the lowest spring constant has the furthest displacement. The sharp vertical lines on the graph indicate the furthest displacement from each particle position. These lines are a vertical asymptote at the furthest displacement limit of each particle position showing an infinite value of this function. For the change of particle position  , it increases the total energy
, it increases the total energy  indicating the decrease of density function
indicating the decrease of density function  towards zero. In fact, dynamically, the difference of the spring constant factor causes the change of the oscillation amplitudes
towards zero. In fact, dynamically, the difference of the spring constant factor causes the change of the oscillation amplitudes  . As a result of this function, a group of the classical harmonic oscillators doing the vibration motion from the equilibrium position
. As a result of this function, a group of the classical harmonic oscillators doing the vibration motion from the equilibrium position  to the largest displacement simultaneously may result in harmonic and no harmonic motions. The smallest
to the largest displacement simultaneously may result in harmonic and no harmonic motions. The smallest  shows that the value of this function remains constant longer than the larger
shows that the value of this function remains constant longer than the larger  with increasing the total energy. This can be studied from the results of demonstration for the four harmonic graphs with determination of the certain position
with increasing the total energy. This can be studied from the results of demonstration for the four harmonic graphs with determination of the certain position  from the equilibrium point
from the equilibrium point  .
.
References
[1] D. A. B. Miller, Quantum Mechanics for Scientists and Engineers, Cambridge: Cambridge University Press, 2007.
[2] Y.-K. Lim, Problems and Solutions on Thermodynamics and Statistical Mechanics, Singapore: World Scientific, 1990.
Permanent Citation