Probability of Long Leads

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
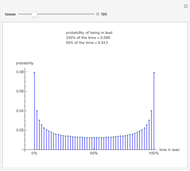
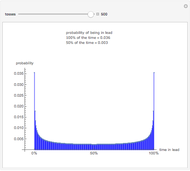
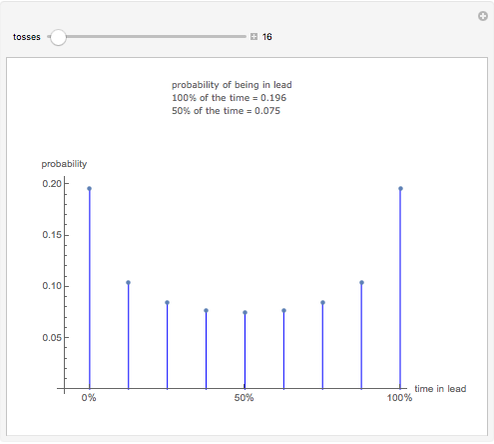
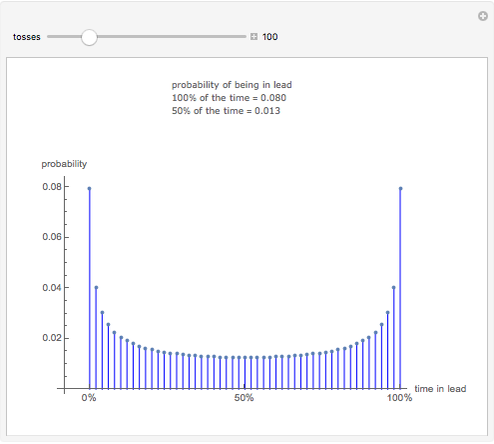
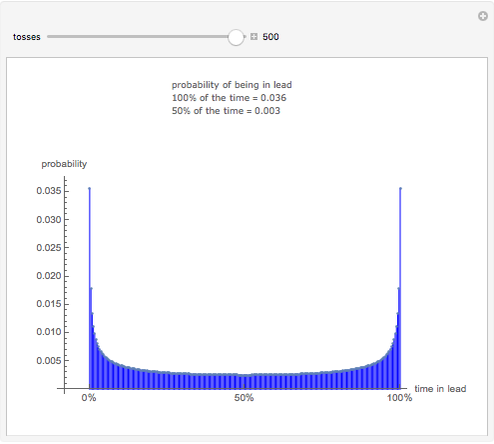
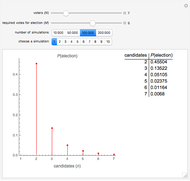
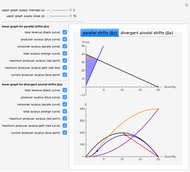
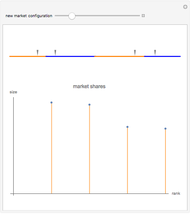
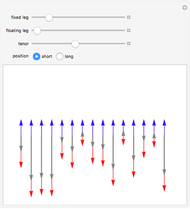
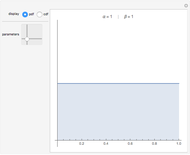
Consider a game in which a fair coin is tossed repeatedly. When the cumulative number of heads is greater than the cumulative number of tails, heads is in the lead. Heads retains the lead until the cumulative number of tails is greater than the cumulative number of heads. The probability distribution above indicates the probability of one side being in the lead for different percentages of the duration of the game. For example, if the coin is tossed 20 times, the probability that heads will be in the lead during the entire course of the game is 0.176, the same as the probability that it will never be in the lead. Surprisingly, the least likely situation is for the two sides to be tied for time in the lead.
Contributed by: Fiona Maclachlan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For even values of  and
and  , the probability that one side is in the lead for
, the probability that one side is in the lead for  out of
out of  tosses is given by:
tosses is given by: 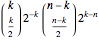
Permanent Citation
"Probability of Long Leads"
http://demonstrations.wolfram.com/ProbabilityOfLongLeads/
Wolfram Demonstrations Project
Published: March 7 2011