Probability of Election in a Vote

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
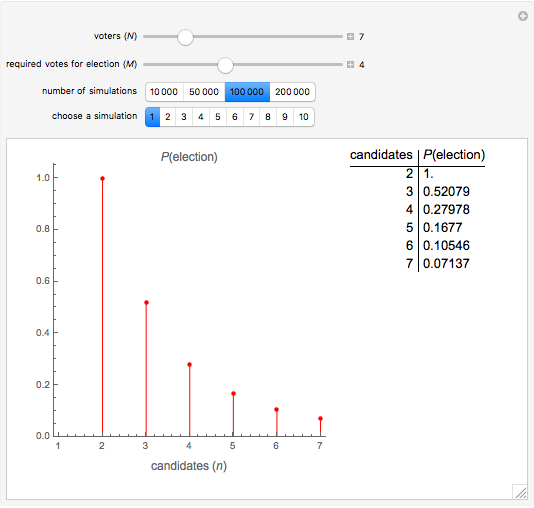
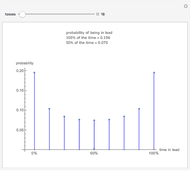
A group of  people wishes to elect one of their members as their leader. Each member of the group can vote for any member in a smaller set of candidates of size
people wishes to elect one of their members as their leader. Each member of the group can vote for any member in a smaller set of candidates of size  . Candidates can vote for themselves. At least
. Candidates can vote for themselves. At least 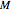 votes are needed to elect a leader. Suppose that each of the
votes are needed to elect a leader. Suppose that each of the  people votes for one of the
people votes for one of the  candidates randomly. The result shows the approximate probability of election as a function of
candidates randomly. The result shows the approximate probability of election as a function of  .
.
Contributed by: Heikki Ruskeepää (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
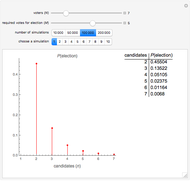
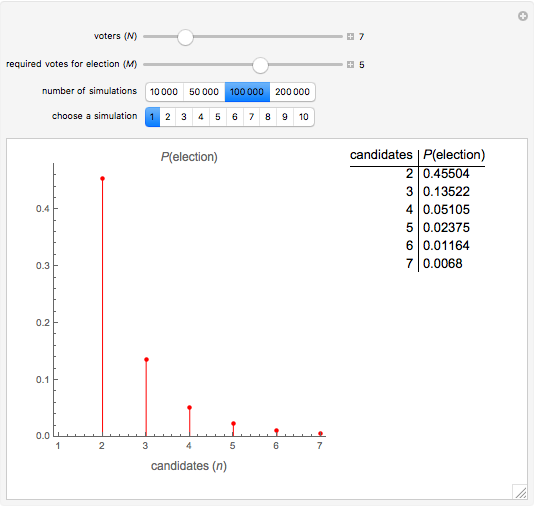
Snapshot 1: There are 7 voters and 5 votes are required for election. For 2 candidates, 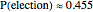 . For 3 candidates,
. For 3 candidates, 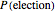 decreases to
decreases to 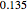 . For 7 candidates (that is, everyone is a candidate), then
. For 7 candidates (that is, everyone is a candidate), then 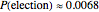 .
.
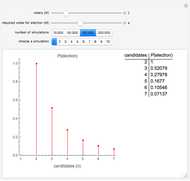
Snapshot 2: Again there are 7 voters, but now only a simple majority (4) is needed for election. This is the so-called imperial election problem [1]. With 2 candidates, one of them always gets at least 4 votes, so that the election is certain. For 3 candidates,  , and for 7 candidates,
, and for 7 candidates, 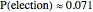 .
.
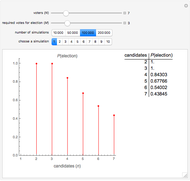
Snapshot 3: There are 7 voters as in snapshot 2, but now only 3 votes are required for election. With 2 or 3 candidates, one of them always gets at least 3 votes, so that the election is certain. For 4 candidates, 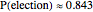 , and even for 7 candidates
, and even for 7 candidates 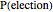 is as high as 0.438.
is as high as 0.438.
Snapshot 4: There are 25 voters, and 17 votes (two-thirds of the votes) are needed for election. This is the so-called pope problem [1] that refers to the papal election in 1513. For 2 and 3 candidates, the probabilities of election are approximately 0.109 and 0.0013, respectively.
The Demonstration is based on problem 19 in [1].
Reference
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
Permanent Citation